Einleitung
Herzlich Willkommen zu meiner interaktiven Artikel: "GPT einfach erklärt". Diese Website basiert auf dem "Transformer Explainer", der ursprünglich von Aeree Cho, Grace C. Kim, Alexander Karpekov, Alec Helbling, Jay Wang, Seongmin Lee, Benjamin Hoover, und Polo Chau am Georgia Institute of Technology entwickelt wurde.
Da ich im deutschsprachigen Raum immerzu gefragt werde, wie ein Sprachmodell eigentlich funktioniert, habe ich mich entschieden, diese fantastische Arbeit ins Deutsche zu übersetzen. Dabei kam auch das von mir entwickelte Open Source KI-Tool RedakTool.ai zum Einsatz. Größtenteils habe ich aber natürlich meinen eigenen Gedanken Form gegeben, da Sprachmodelle nicht deduktiv denken, und somit auch nicht wirklich intelligent arbeiten können (dazu später im Detail mehr).
Beim Verfassen dieses Artikels war es mir ferner ein großes Anliegen, den Text auch stark zu erweitern um ihn in seiner Verständlichkeit zu verbessern. Ich bin der Meinung, dass ein Verständnis der Konzepte hinter GPTs für alle Menschen, unabhängig von Herkunft, Alter und Bildungsgrad erreichbar und frei zugänglich sein sollte. Diese Technologie hat bereits ein viel zu großes Potenzial gezeigt und birgt viel zu große Risiken, als dass man ihr Verständnis nur einer kleinen Gruppe von Experten überlassen sollte. In einer perfekten Welt würde die Funktionsweise von GPTs vielleicht sogar in der Schule gelehrt werden. Die ein oder andere Schüler*in könnte sich so dazu entscheiden, das Denken und ihre Kreativität vielleicht doch nicht allein der Statistik und dem Zufall zu überlassen.
Für eine schnellere Ausführung und kleinere Download-Größe habe ich das ursprüngliche GPT-2-Modell außerdem quantisiert. Auch dieser Prozess ist hier ausführlich und allgemeinverständlich beschrieben. Da das GPT-2-Modell direkt hier im Browser ausgeführt wird, können Sie jeden Schritt der im Modell ausgeführt wird, einzeln und interaktiv nachvollziehen, indem Sie über die Überschriften und Grafiken hovern oder auf die entsprechenden Buttons klicken. Die Pfeil-Buttons stellen Sprungmarken dar, die Sie direkt zu den entsprechenden Abschnitten führen.
Bei Fragen oder Anmerkungen schreiben Sie mir bitte über das Feedback-Formular. Ich freue mich bereits auf Ihre Nachrichten und versuche, diesen Artikel stetig zu verbessern, zu aktualisieren und zu erweitern.
Was ist ein Transformer?
Wenn die Rede von "Transformern" ist und insbesondere, wenn über "GPTs" gesprochen wird, spricht man von Transformer-basierten, große Sprachmodellen. Diese fallen in die Kategorie des Maschinelles Lernens (Machine Learning; ML) und insbesondere unter den Begriff "Neuronale Netze". Der Begriff "Transformer-Architektur", welcher in diesem Zusammenhang oft genannt wird, bezieht sich dabei nur auf die Art und Weise des Aufbaus, also der spezifischen Konstruktion eines bestimmten neuronalen Netzes. Dabei geht es um die mathematischen Grundlagen der Netz-Architektur die den Lernprozess (Training) und die Anwendung (Inference) des Modells bestimmen.
Viele der führenden großen Sprachmodelle bedienen sich aktuell (Stand August 2024) der Transformer-Architektur. Oft wird daher ganz allgemein von "Transformern" gesprochen, wenn von KI-Modellen die Rede ist, die auf dieser Architektur beruhen. Die erste Veröffentlichung der Transformer-Architektur erfolgte 2017 mit dem Paper "Attention is All You Need". Seitdem stellt diese Architektur die erste Wahl für Deep Learning-Modelle ("Mehrschichtige Lernmodelle") wie beispielsweise OpenAIs GPT und ChatGPT, Metas Llama, Anthropics Claude und Googles Gemini-Modelle dar. Auch moderne Vektor-Einbettungsmodelle, von denen wir später noch mehr lesen werden, bedienen sich der Transformer-Architektur.
Die Transformer-Architektur hat jedoch nicht nur die Forschung- und Entwicklung von KI-Sprachmodellen stark beeinflusst, sondern gab und gibt auch Impulse für KI-Modelle anderer Domänen, wie Audio-Generierung (z.B. Suno.ai), Bilderkennung, die Vorhersage von Protein-Sturkturen oder auch Gaming-Strategien. Wie sich unschwer erkennen lässt, hat die Transformer-Architektur eine Tragweite, die sich über viele Domänen hinweg entfaltet.
Training eines GPT
Damit mithilfe der Transformer-Architektur und einer großen Menge an Textdaten ein großes Sprachmodell entstehen kann, findet ein Prozess statt, der als Training bezeichnet wird. Im ersten Schritt wird ein so genanntes Pre-Training durchgeführt, bei dem das Modell auf einer großen Menge ungekennzeichneter Textdaten trainiert wird. Hierfür wird ein Dataset, also eine große Menge an Texten verschiedener Sprachen aus unterschiedlichen Datenquellen zusammengestellt. Im Rahmen von GPT-2 handelte es sich um 40 GB Text aus 8 Millionen Dokumenten von 45 Million Webseiten welche auf Reddit.com positiv bewertet wurden. Durch Web-Crawlings wurden die relevanten Textinhalte der Webseiten abgerufen und anschließend mittels klassischen, statistischen NLP- und ML-Verfahren, also maschinellen Lernverfahren zur Verarbeitung natürlicher Sprache, aufbereitet.
Anschließend wurden dieses Dataset verwendet, um das eigentliche Sprachmodell zu trainieren. Dadurch, dass ein solches Modell nicht während seiner Anwendung (also der Generierung von Text) entsteht, sondern bereits vorab, spricht man von einem vortrainierten (pretrained) Modell. Das Ergebnis dieses Trainingsprozesses wird als generativer, vortrainierter Transformer (Generative Pre-trained Transformer, GPT) bezeichnet. Ein GPT besteht also nicht nur der Transformer-Architektur, sondern ganz elementar aus seinen Trainingsdaten, die neben verschiedenen anderen Optimierungen bei der Daten-Vorverarbeitung, beim Training und bei der Anwendung des Modells, maßgeblich über die Text-Generierungsqualität des Sprachmodells entscheiden.
Um die Funktionsweise eines GPT-Modells zu verstehen, ist es wichtig, die einzelnen Schritte des Trainingsprozesses zu kennen. Es folgt daher eine sehr abstrakte und vereinfachte Darstellung des Trainings- und Anwendungsprozesses eines GPT-Modells:
- Tokenisierung (Tokenization) Beim Prozess des Trainings lernt das Modell, Muster, Strukturen und Zusammenhänge in der Sprache zu erkennen. Um maschinell aus Texten lernen zu können, muss der Eingabetext zunächst in eine Form gebracht werden, die das Modell verarbeiten kann. Dieser Prozess wird Tokenisierung genannt. Wörter, Interpunktionszeichen sowie Sonderzeichen werden mittels eines so genannten Tokenizers, also eines statistischen Wort- und Zeichentrenners, in so genannte Tokens zerlegt. Diese stellen das eigentliche "Vokabular" des Sprachmodells dar.
- Einbettung (Embedding) Anschließend werden diese Tokens einzeln in Vektorform, also in eine mathematische Beschreibung der semantischen als auch syntaktischen Bedeutung der Worte und Zeichen, umgewandelt. Dieser Prozess wird auch als Einbettung (Embedding) bezeichnet. Für jeden möglichen Token entsteht beim Trainingsprozess schrittweise, in so genannten "Epochen", eine stetig optimierte Einbettung.
- Tiefes Lernen (Training) Ebenso wird beim Training eines Sprachmodells ein künstliches neuronales Netz in Schichten trainiert, welches letztlich lediglich die bedingten Eintrittswahrscheinlichkeiten modelliert, welcher Token wahrscheinlich als nächstes auf eine Sequenz von Eingabetokens folgen könnte. Dieser Trainingsprozess setzt sich aus mehreren Schritten zusammen, wie beispielsweise dem Vortraining (Pre-training), der Feinabstimmung (Fine-Tuning), dem verstärktem Lernen durch menschliches Feedback (RLHF) sowie weiteren Methoden des maschinellen Lernens.
Anwendung eines GPT
Wird das Sprachmodell schließlich angewendet, werden nacheinander einige Arbeitsschritte in einem Verfahren abgearbeitet, das als "Inferenz" (Inference) bekannt ist. Es ist wichtig zu verstehen, dass die Bestimmung eines jeden Tokens in der Ausgabe des Modells auf den vorherigen Tokens basiert. Dadurch entsteht eine Art "Kettenreaktion" von Token zu Token, die letztlich den gesamten Text generiert. In Fachkreisen wird dieses Verhalten eines Systems als "Autoregression" bezeichnet. Der Prozess wird so lange fortgesetzt, bis eine vorab festgelegte Tokenanzahl erreicht ist (Maximum Output Tokens) oder ein spezielles Ende-Token generiert wird, dass aussagt, die Inferenz zu stoppen, weil es keine weiteren sinnvollen Tokens mehr für den gegebenen Eingabetext zu erstellen gibt.
Sie können übrigens jeden der Schritte einzeln im Diagramm nachvollziehen. Durch einen Klick auf den "Generieren"-Button wird der Prozess für einen weiteren Autoregerationsschritt, also die Inferenz zur Bestimmung des nächsten Wortes im Satz, ausgeführt.
Die folgenden Arbeitsschritte werden der Reihe nach ausgeführt:
- Tokenisierungs-Modell laden: Das vortrainierte Tokenisierungs-Modell und dessen Konfiguration wird in den Speicher geladen. Der GPT-2 Tokenizer dieses Modells ist 1.36 MB groß, die Konfiguration lediglich 26 Bytes.
- Tokenisierung: Der Eingabetext wird durch den Tokenizer in Tokens aufgetrennt. Mehr dazu im Abschnitt "Wie funktioniert ein Tokenizer?".
- GPT-Modell laden: Das vortrainierte GPT-Modell wird in den Speicher geladen. Im Falle des hier im Browser ausgeführten Modells sind das 167 MB.
- Vektor-Einbettung: Die resultierenden Token-IDs werden in Vektor-Einbettungen gewandelt. Mehr dazu im Abschnitt "Vektor-Einbettungen".
- Transformer-Block/Aufmerksamkeits-Mechanismus Die finalen Vektor-Einbettungen werden pro Token in drei Vektoren transformiert (Anfrage, Schlüssel, Wert), die sich aus den im Training erlernten Gewichten und Verzerrungen ergeben. Anschließend werden sie schrittweise durch den Aufmerksamkeits-Mechanismus (Attention Mechanism) verarbeitet, der letztlich ein Scoring ergibt, dass aussagt, wie viel Fokus auf jedem der Eingabetokens liegen sollte, wenn die Ausgabe generiert wird. Dieser ahmt die menschliche Aufmerksamkeit nach, indem er die Relevanz der semantischen Bedeutung der Worte untereinander berechnet. Mehr dazu im Abschnitt "Aufmerksamkeits-Mechanismus".
- Mehrlagiges Perzeptron (MLP): Das Mehrlagige Perzeptron (MLP) ist ein mehrschichtiges neuronales Netz, das die vom Aufmerksamkeitsmechanismus verarbeiteten Vektor-Einbettungen durch mehrere Schichten transformiert. In der letzten Schicht entstehen unnormalisierte Score-Werte die für die anschließende Bestimmung der Wahrscheinlichkeiten der Ausgabetokens verwendet werden. Mehr dazu im Abschnitt "Mehrlagiges Perzeptron".
- Ausgabe: Die Logits werden oftmals mit Hyperparametern wie "Temperature" beeinflusst, um die Wahrscheinlichkeiten der Ausgabetokens nachzujustieren. Anschließend werden sie mit der Softmax-Funktion in Wahrscheinlichkeiten umgewandelt, um eine sotierte Liste mit Tokens zu erstellen, die die beste Fortsetzung des Eingabetextes darstellen. Schließlich wird der beste Token anhand seiner Token-ID und mittels des Vokabulars des trainierten Tokenizers, in menschenlesbaren Text zurückgewandelt. Mehr dazu im Abschnitt "Mehrlagiges Perzeptron".
Die Frage nach Bewusstsein und echter Intelligenz
Es ist wichtig zu verstehen, dass ein GPT-Modell, wie es hier beschrieben wird, keine bewusste Intelligenz besitzt. Es ist ein mathematisches Modell, das auf Basis von Statistiken und Wahrscheinlichkeiten arbeitet. Es kann keine eigenen Gedanken oder Emotionen haben, sondern lediglich Muster in Texten erkennen und diese in neuen Texten wiedergeben. Die Qualität der Texte, die ein GPT-Modell generiert, hängt daher stark von der Qualität der Trainingsdaten ab. Die Texte, die ein GPT-Modell generiert, sind also letztlich nur eine Art "Spiegel" der Texte, die ihm während des Trainings gezeigt wurden. Da ein GPT-Sprachmodell nicht in der Lage ist, deduktiv zu denken, kann es auch keine "echte" Intelligenz besitzen, sondern diese nur durch sampling von durch menschlicher Intelligenz geprägter Texte simulieren. Mehr zu diesem Thema finden Sie im Abschnitt "Über Halluzinationen, Induktion und Deduktion".
Ökonomische und Ökologische Aspekte
Wie Sie sehen können, ist die Funktionsweise eines GPT-Sprachmodells komplex und basiert auch nach dem Training noch auf einer Vielzahl von mathematischen und statistischen Verfahren, die in der Praxis auf Servern mit leistungsstarken Tensor-Kernen (TPUs) und Grafikprozessoren (GPUs) ausgeführt werden. Es ist daher nicht verwunderlich, dass die Entwicklung und der Betrieb solcher Modelle mit hohen Kosten verbunden ist, die neben dem Energieverbrauch auch aus den Investitionskosten für die Hardware und den Betrieb der Server resultieren. Mehr zu diesen Themen finden Sie im Abschnitt "Exkurs: Wirtschaftlichkeit und Klimaschutz".
Was sind Vektordatenbanken?
Ein wichtiger Aspekt bei der Anwendung von GPT-Modellen ist die Verwendung von Vektordatenbanken. Diese speichern Daten nicht direkt, sonern wandeln sie mit hilfe eines Vektor-Einbettungsmodells zunächst in Vektor-Einbettungen um. Diese können nach der Speicherung mit Hilfe spezieller Suchalgorithmen effizient durchsucht werden. Dabei ist der Hauptunterschied zu klassischen Datenbanken, dass die Suche nicht auf exakten Übereinstimmungen basiert, sondern auf der semantischen Ähnlichkeit der Vektoren. Es kann also beispielsweise nach ähnlichen Texten gesucht werden, die nicht exakt den Suchbegriff enthalten oder sogar in einer anderen Sprache verfasst sind. Mehr dazu im Abschnitt "Vektordatenbanken".
Was ist Prompt Engineering?
Ein weiterer wichtiger Aspekt bei der Anwendung von GPT-Modellen ist das sogenannte "Prompt Engineering". Der Begriff "Prompt" steht dabei schlicht und einfach für den Eingabetext, den Sie das GPT-Modell verarbeiten lassen. "Engineering" ist in diesem Kontext nichts weiter, als das Wissen über die Funktionsweise, wie ein GPT arbeitet, verbunden mit dem Wissen, wie man solche Prompts am besten formuliert, um ein bestimmtes Ziel zu erreichen - also beispielsweise, um Texte in einer bestimmten Sprache, zu einem bestimmten Thema oder in einer bestimmten Form zu generieren.
Genau genommen verwenden Sie beim Chatten mit ChatGPT & Co. also bereits schon Prompt Engineering, wenn Sie dem Modell eine Frage stellen oder ein Thema vorgeben. Je nachdem, wie genau, in welchem Umfang und in welcher Reihenfolge Sie den Prompt formulieren, wird das KI-Modell jedoch unterschiedlich darauf reagieren. Das Verhalten ist auch abhängig vom gewählten Modell und dessen Trainingsdaten. Mehr dazu im finden Sie im Abschnitt "Prompt Engineering".
Was sind RAG-Workflows?
Mit Hilfe von RAG-Workflows (Retrieve, Answer, Generate) können GPT-Sprachmodelle auch für spezielle Anwendungsfälle eingesetzt werden, also nicht bloß für einen lustigen Chat am Küchentisch. In der Regel werden bei RAG-Flows Daten abgerufen, die beim Training des Sprachmodells nicht enthalten waren - bei denen das Sprachmodell demnach halluzinieren würde. Daher werden die abgerufenen Daten als Text in einen durch Prompt Engineering optimierten Eingabetext eingefügt. Anschließend wird die Ausgabe des Sprachmodells verwendet, um meist weitere Schritte im gesamten Workflow durchzufühen, die ebenfalls wieder das Sprachmodell einbeziehen können. RAG-Workflows werden ebenfalls oft in Verbindung mit Vektordatenbanken verwendet, um relevante Informationen zwischenspeichern und wieder abrufen zu können. Mehr dazu im Abschnitt "RAG-Workflows".
Multi-Modale Sprachmodelle
TODO: LLaVA erklären
Experten-Sprachmodelle
TODO: Mixture of Experts / Mixtral erklären
Open Source Sprachmodelle: Sind sie wirklich frei?
TODO: Erklären was Open Source bedeutet, was Open Weights meint und wie es sich von echtem Open Source unterscheidet.
FAQ: Häufig gestellte Fragen
TODO: - Kann ich selber ein GPT-Modell trainieren? - Kann ich selber ein GPT-Modell betreiben? - Wie integriere ich ein GPT-Modell in meiner App/Webseite?
Hintergrundwissen
Zunächst haben wir uns einen Überblick über alle relevanten Themen im Bereich generativer KI mit Transformer-Modellen und insbesondere GPT-Sprachmodellen verschafft. Die grundsätzliche Funktionsweise eines GPT-Modells sollte nun bereits etwas klarer sein. In den folgenden Abschnitten werden alle zuvor erwähnten Fachbegriffe detailliert erläutert, Algorithmen anhand von greifbaren Beispielen und Analogien erklärt und Konzepte vertieft. Jeder Abschnitt baut dabei auf den vorherigen auf, sodass Sie am Ende ein umfassendes Verständnis für die Funktionsweise und Anwendung von GPT-Modellen haben sollten.
Wie funktioniert ein Tokenizer?
Wie Sie sich vielleicht bereits vorstellen können, kann auch ein Tokenizer mittels statistischer Methoden und maschinellem Lernen automatisch auf Basis von beliebigen Texten trainiert werden. Dazu werden die Texte in kleinere Bestandteile wie Wörter, Teilworte oder sogar einzelne Zeichen zerlegt. Der Tokenizer lernt dabei, wie diese Bestandteile in der Sprache auftreten und wie sie am besten segmentiert werden können. Ziel ist es, den Text so zu zerlegen, dass er für das Sprachmodell möglichst effizient und verständlich verarbeitet werden kann. Der Tokenizer passt sich während des Trainings an, um eine optimale Balance zwischen der Zerlegung in zu kleine oder zu große Einheiten zu finden.
Der BPE-Algorithmus
Ein typischer Vertreter für einen statistischen Tokenization-Algorithmus ist BPE (Byte Pair Encoding). BPE ist ein Verfahren zur Vokabular-Kompression, das häufig vorkommende Zeichen oder Zeichenpaare in einem Text identifiziert und diese zu neuen Kombinationen zusammenführt. Diese Methode ist besonders effektiv in Texten, die in UTF-8 kodiert sind, da dieses Format eine variable Byte-Länge pro Unicode-Symbol verwendet (von einem bis zu vier Bytes). Dies ermöglicht es BPE, effizient mit Texten in unterschiedlichsten Sprachen und Symbolsets zu arbeiten.
Dieser Algorithmus beginnt zunächst damit, das Vokabular aus dem Trainingstext aufzubauen, indem alle einzigartigen Zeichen erfasst. Für unseren Beispielsatz könnte das initiale Vokabular so aussehen:
["H", "e", "l", "o", ",", "W", "r", "d"]. Anschließend analysiert BPE den Text, um die häufigsten benachbarten Zeichenpaare zu finden.
Ein passende Beispiel könnte "ll" in "Hello" sein. Dieses kommt auch häufig, also mit hoher Frequenz, in anderen Worten vor. "Hell" wäre hier als Beispiel zu nennen, oder "mellow".
Die Frequenz der Vorkommnisse wird automatisch und Schrittweise durch Zusammensetzen von Vokabel-Teilen zu neuen Vokabeln getestet.
So wird "He" und "ll" beispielsweise durch BPE zu "Hell" kombiniert. Dessen Frequenz wird im Trainingstext gemessen. Da "Hell" im Trainingstext oft vorkommt, wird es dem Vokabular des Tokenizers hinzugefügt.
Kombiniert BPE im nächsten Schritt "Hell" mit "ll" kommt keine hinreichende Frequenz für "Hellll" zustande. Diese Vokabel wird verworfen.
Der Prozess stoppt, wenn keine weiteren neuen Vokabeln mit minimaler Frequenz im Trainingstext zu finden sind oder wenn entweder die maximale, vorab festgelegte Vokabulargröße oder die maximale Anzahl an Kombinationsschritten erreicht ist.
Im Ergebnis findet man im Vokabular eines BPE-basierten Tokenizers sehr viele Wörter die im Trainingstext vorkommen, aber auch Teilwörter mit hoher Frequenz. Dies ermöglicht es, dass der Tokenizer auch Worte verarbeiten kann, die zuvor nicht im Training vorkamen ("Out-of-Vocabulary", OOV), indem er sie in bekannte Teilworte oder Zeichenketten zerlegt.
Da sich diese von bekannten Vokabeln unterscheiden lassen sollten, kommen je nach BPE-Implementation Prefixe im Vokabular vor. Das hier verwendete GPT-2 Tokenizer Vokabular kann
hier als tokenizer.json-Datei abgerufen werden.
Suchen Sie in dieser JSON-Datei doch einmal nach dem Wort "Hello". Speziell für GPT-2 wurde BPE übrigens weiter angepasst, um ineffiziente Tokenisierungen zu verhindern, was die Modellflexibilität und Effizienz verbessert.
So wurde verhindert, dass BPE Zeichen unterschiedlicher Kategorien zusammenführt, mit Ausnahme von Leerzeichen, was die Kompressionseffizienz signifikant verbessert, ohne Wörter unnötig in viele Token zu zerlegen. Quelle: "Language Models are Unsupervised Multitask Learners", OpenAI
Mehrsprachigkeit in Sprachmodellen beginnt mit dem Tokenizer
Es sollte bereits klar geworden sein, dass ein Tokenizer, der ausschließlich oder vornehmlich auf Basis von englischem Text trainiert wurde, primär nur englische Eingabetexte in sinnvolle Tokens zerlegen kann, welche die syntaktische Bedeutung des Textes und der Interpunktion des Eingabetextes wiederspiegeln. Probieren Sie es gerne einmal selbst aus. GPT-2, das Modell, dass in diesem Artikel zum Einsatz kommt, wurde nicht auf deutschen Texten trainiert. Wenn Sie also einen deutschen Text eingeben, wird der Tokenizer selten korrekt in Worte der Deutschen Sprache trennen können, sondern in Teilworte und Zeichen, die im englischen Vokabular des Tokenizers vorkommen.
Heute ist es üblich, Sprachmodelle mit starken Fähigkeiten für Mehrsprachigkeit zu trainieren. Ein wegweisendes "Cross-lingual Language Model Pretraining", welches Methoden zum verbesserten Training von Sprachmodellen beschreibt, wurde 2019 von Facebook AI Research (Meta AI) vorgestellt. Es bildete die Grundlage des XLM-RoBERTa GPT-Sprachmodells, welches seinerseits ein Vorläufer der LLaMA-Modellreihe von Meta AI ist.
Dieser Artikel bezieht sich jedoch exemplatisch auf das GPT-2-Modell von OpenAI, welches im Februar 2019 veröffentlicht wurde.
Tokenisierungs-Beispiel: "Hello, World" (Real World)
Analysieren wir anhand eines Beispiels die genaue Funktionsweise des Tokenizers. Sie können diesen Text auch oben in die Eingabezeile eingeben und auf "Generieren" klicken. Anschließend ergibt sich links die Wortliste unter "Einbettungen". Wenn Sie auf ein Wort klicken, öffnet sich die Detailansicht mit den jeweiligen Token-IDs.
| Token-ID | Wort |
| 6318 | Hello |
| 7874 | , |
| 4015 | World |
Anstatt "Hello, World", lernt und verarbeitet das neuronale Netz also 6318, 7874, 4015. Da für das Erfassen der syntaktischen und semantischen Bedeutung von Texten auch die Reihenfolge der Worte, Interpunktionszeichen und Sonderzeichen bedeutsam ist, wird auch die Position jedes einzelnen Tokens in einem Eingabetext für die Verarbeitung assoziiert. Dies wird als Positions-bezogene Kodierung bezeichnet ("Positional Encoding").
| Token-ID | Wort | Position |
| 6318 | Hello | 0 |
| 7874 | , | 1 |
| 4015 | World | 2 |
Beim Sortieren wird in der Informatik in der Regel mit der Zahl 0 begonnen, da sie genauso einen Wert, also eine Information ausdrückt, wie jede andere Zahl. Die tabellarische Darstellung ist daher korrekt, auch wenn Sie für Sie vielleicht ungewöhnlich erscheinen mag.
Vektor-Einbettungen (Vector Embeddings)
Im letzten Abschnitt hatten wir bereits ein Fachwort verwendet, welches noch nicht hinreichend erklärt wurde: Einbettungen (Embeddings). Was unterscheidet die Liste aus Token-IDs von Einbettungen?
Zunächst einmal sollte erwähnt werden, dass je nach KI-Modell, von dem gesprochen wird, auch das Wort "Einbettungen" (Embeddings) eine andere Bedeutung haben kann. So unterscheiden sich Vektor-Einbettungen, wie sie in großen Sprachmodellen erzeugt werden, um Schritt für Schritt zur Textgenerierung verwedendet zu werden, von Vektor-Einbettungen, die mit einem reinen KI-Vektor-Einbettungs-Modell erzeugt werden, um eine Ähnlichkeitssuche zwischen Texten, Text-Klassifizierung oder Sortierung von Suchergebnissen nach Relevanz umzusetzen. Auch wenn die Idee, die hinter Vektor-Einbettungen steht bei jedem KI-Modell die selbe ist, nämlich Informationen, die wir als Mensch über unsere Sinnesorgane wahrnehmen, in eine mathematisch interpretierbare Form zu bringen, unterscheiden sich die mathematischen Ansätze je nach Modell teilweise stark. Doch wie sehen denn nun eigentlich Vektor-Einbettungen aus und wie werden sie genau erzeugt?
Wie wir bereits gelernt haben, besteht der initiale Input vor der eigentlichen KI-Modell-Verarbeitung aus einer Liste von Token-IDs und deren Positionen. Diese Informationen repräsentieren den Eingabetext in einer kodierten und grundlegende diskreten Form. Worte und Zeichen wurden bereits eindeutigen Zahlen zugeordnet. Leider genügt dies jedoch noch nicht, um die semantische Bedeutung von Texten mathematisch zu erfassen. Der Satz: "I left my phone on the left side of the table." beinhaltet z.B. zwei mal das Wort "left", doch in beiden Fällen hat das Wort eine völlig andere Bedeutung im jeweiligen Kontext. Wie genau können wir so ein Problem lösen?
Als erstes sollte gesagt sein, dass beim Training von GPT-Sprachmodellen eine so genannte Vektor-Einbettungs-Übersetzungs-Matritze sowie eine Positions-Übersetzungs-Matritze trainiert wird. Diese Matritzen haben eine festgelegte Größe und funktionieren letztlich wie eine Tabelle, in der wir für jede Token-ID eine Vektor-Repräsentation nachschlagen können. Auch für jede Position, die vorkommen kann, wurde beim Training des Sprachmodells bereits ein bestimmter Positions-Vektor vordefiniert. Die Token-Matrix hat dabei genau so viele Einträge, wie das Vokabular des Tokenizers groß ist. Für jede Token-ID findet sich in dieser Matrix also ein Eintrag. Die Positions-Matrik hat genau so viele Einträge, wie die maximale Input-Token-Anzahl für das Sprachmodell definiert ist. Die Maximale Input-Token-Anzahl (Max Input Tokens) ist auch als Kontext-Größe eines Sprachmodells bekannt. Egal welche Token-ID also im Input gefunden wird, können wir einen Token-Vektor aus der Matrix abrufen und egal an welcher Position der Token steht (es ist ja lediglich eine begrenzte Anzahl), können wir einen passenden Positions-Vektor nachschlagen. Doch wie sehen die vorab definierten Vektoren genau aus und welche Informationen kodieren sie?
Um das zu verstehen, sollten wir uns kurz einige Gedanken dazu machen, wie ein Computer überhaupt Bedeutungsbeziehungen mehrerer Worte zueinander abbilden könnte. Wir als Menschen haben dafür ein intuitives Verständnis. Uns ist bewusst, dass die Worte "Woman" und "Queen" einen Bedeutungskontext teilen - denn es ist ziemlich klar, dass es hier um das weibliche Geschlecht geht, dass beide Worte semantisch miteinander verbindet. Auch die Worte "Man" und "King" teilen einen geschlechtlichen Bedeutungskontext. "King" und "Queen" teilen sich den Monarchie-Bedeutungsraum. Dieser hat jedoch eine ganz andere Begründung, als der Bedeutungsraum von "Woman" und "Man", die biologische Geschlechter darstellen. Soll ein Computer solche semantischen Bedeutungsbeziehungen von Vokabeln in einem Vokabular untereinander abbilden können, benötigen wir hierfür eine mathematisch effiziente Darstellungsform. Hierfür hat man Vektoren als die bisher effizienteste mathematische Repräsentationsform erkannt.
Was sind Vektoren und wie werden sie für Einbettungen eingesetzt?
Versetzen wir uns kurz zurück in die Grundschule. Als wir das erste mal mit dem Messen von Abständen begonnen haben, verwendeten wir dafür ein Maßband. Wir lernten, dass wir Abstände in Einheiten unterteilen können. Das hat den Vorteil, dass aus einer undefinierbaren Länge auf einmal so etwas wie z.B. 3 cm werden. Durch die Unterteilung in kleinere Einheiten, werden Abstände zählbar. Am Zahlenstrahl können wir Zahlen in Ganzzahlen unterteilen und so beispielsweise messen, wie weit die 2 von der 5 entfernt ist. Der Abstand, also die Differenz zwischen 2 und 5 ist 3. Wir können also mathematisch darstellen, dass die 2 weiter von der 5 entfernt ist, als die 2 von der 4.
Allerdings betrachten wir diese Abstände momentan nur eindimensional. Wörter haben jedoch vielfältige semantische Beziehungen zueinander, die in mehr als nur einer Dimension erfasst werden müssen.
Beispielsweise sollte "Tee" ("tea", Token-ID: 2902) nah bei "Honig" ("honey", 286) liegen, aber "Honig" auch nah bei "Bienen" ("bees", 5998),
die wiederum nah bei "Biene" ("bee", 7975), dem Singular von "Bienen", sein sollten.
Wie bilden wir all diese Beziehungen und ihre Nähe zueinander mathematisch ab?
Im Grunde ist es einfach: Anstatt den Abstand zweier Zahlen auf einem Zahlenstrahls messen, definieren wir einfach, dass der Zahlenstrahl jeweils immer von -1 bis 1 lang ist. Hier sprechen wir von einer Skala, kurz: [-1..1].
Der Zahlenraum zwischen -1 und 1 besteht aus Fließkommazahlen, also rationalen Zahlen mit Nachkommastellen. Eine 0 entspricht somit der Mitte, also 50% der Länge des Zahlenstrahls. Eine -1 entspricht 0% und eine 1 entspricht 100%.
Stellen wir uns nun einen Pfeil vor, der immer bei -1 beginnt und irgendwo zwischen -1 und 1 endet. Dieser Pfeil zeigt also in eine Richtung und bedingt durch seine Länge genau auf eine Zahl zwischen -1 und 1.
Solch einen Pfeil nennen wir einen Richtungsvektor oder einfach "Vektor(...)". Ein Vektor kann jedoch nicht nur in eine Richtung zeigen. Je mehr Pfeile wir dem Vektor hinzufügen, in desto mehr Richtungen kann der Vektor zeigen.
Wir sprechen hier auch von Dimensionen, also der Dimensionalität eines Vektors, denn in jede mögliche Richtung zeigt immer nur ein Pfeil.
Ein eindimensionaler Vektor (1D) ist also im Grunde nichts weiter als ein Pfeil der in eine Richtung zeigt: Vektor(1, [0]).
Für eine Aussage, ob Honig süß ist, könnten wir für die Token-ID 286 und die Bedeutung "süß" also z.B. 0.8 speichern. Für die Bedeutung "flüssig" könnten wir 0.6 speichern.
Wir bräuchten nun zwei Pfeile. Es entsteht also ein 2D-Vektor, ein Vektor der in zwei Richtungen zeigt. Er beschreibt also zwei Dimensionen. Die beiden Zahlen die wir speichern, nennen wir Elemente des Vektors.
Der Einbettungs-Vektor für "Honig" könnte also so aussehen: Vektor(2, [0.8, 0.6]). Wie Sie feststellen, haben die Elemente eine Reihenfolge.
Die Reihenfolge ist wichtig, denn sie gibt an, welche semantische Bedeutung die Zahl repräsentiert. Möchten wir später die Bedeutung mehrerer Worte untereinander vergleichen,
gehen wir davon aus, dass die Reihenfolge der Bedeutungen in allen Vektoren gleich ist, damit wir nicht "flüssig" mit "süß" verwechseln.
Natürlich genügt ein 2D-Vektor nicht, um alle semantischen Beziehungen zwischen Wörtern abzubilden. In der realen Welt benötigen wir oft hochdimensionale Vektoren, also Vektoren, die in sehr viele Richtungen zeigen.
So entstehen Vektoren mit 768 Dimensionen (Pfeilen), wie sie in GPT-2 verwendet werden. Jede Dimension eines Vektors repräsentiert dabei jeweils eine semantische Eigenschaft, und der Vektor speichert den Abstand für jede dieser Eigenschaften.
Der echte Token-Einbettungs-Vektor für das Wort "Data" ist z.B. wie folgt gespeichert: Vektor(768, [0.14001226425170898, -0.05600490793585777, 0.11200981587171555, ...]). Sie können diese Vektoren auch in der Detailansicht "Einbettung" neben den "Token" einsehen, wenn sie mit der Maus über die Token-IDs hovern.
Nachschlagen der Einbettungs-Vektoren
Wie Sie vielleicht festgestellt haben, sind wir beim Verständnis der Verarbetung der Texteingabe für ein Sprachmodell noch nicht sehr weit gekommen. Wir haben gelernt, dass ein Tokenizer die Eingabe in eine Liste von Token-IDs und deren Positionen zerlegt. Wir wissen auch bereits, dass beim Training des Modells für jede Token-ID eine Vektor-Repräsentation gelernt wurde, die die semantische Bedeutung des Tokens, also des Wortes, des Satzzeichens, Emojis etc. kodiert. Doch wie kommen wir nun an diese Vektoren heran, wenn wir das Modell anwenden, also Text generieren möchten, doch nur eine Token-ID kennen?
Eingangs hatten wir bereits gelernt, dass beim Training des Sprachmodells auch Einbettungen für Tokens gelernt wurden. Diese werden als Vektoren in einer Liste gespeichert, die so viele Zeilen hat, wie das Vokabular des Tokenizers groß ist. In der ersten Spalte wird die Token-ID gespeichert und in der zweiten Spalte der jeweilige, vortrainierte Einbettungs-Vektor für den Token. Eine solche Liste an Vektoren nennen wir eine Matritze oder Matrix.
Die Vektoren in dieser Matrix werden jedoch nicht an beliebigen Positionen abgespeichert, sondern nach Token-IDs sortiert, sodass es zwischen den Zeilen keine Lücken gibt. Dadurch lässt sich für das gesamte Tokenizer-Vokabular von Token 0 bis Token 50.256 jeweils ein Einbettungs-Vektor finden. Da wir durch die Sortierung wissen, dass sich der Einbettungs-Vektor für die Token-ID 0 in der ersten Zeile der Matrix befindet (für Computersysteme ist die 0 die erste gültige Zahl), und jeder andere Token in der Matrix an der Position abgespeichert ist, die der Token-ID entspricht, können wir den Einbettungs-Vektor für jede Token-ID einfach nachschlagen, indem wir lediglich die Position abfragen, die der Zahl der Token-ID entspricht.
So kommen wir von einer Liste an Token-IDs, die vom Tokenizer ausgegeben wird, zu einer Liste an Einbettungs-Vektoren, die sich jedoch in dieser Form noch nicht zur direkten Verwendung mit dem trainierten neuronalen Netz eigent.
Die Reihenfolge macht den Unterschied
Im Rahmen der großen Sprachmodelle wie GPT-2 galt es ferner noch ein weiteres Problem zu lösen:
Das selbe Wort oder Zeichen, das in einem Satz an unterschiedlicher Stelle vorkommen kann, könnte eine jeweils völlig unterschiedliche semantische Bedeutung inne haben.
Im Eingangs angeführten Beispiel "I left my phone on the left side of the table." hat das Wort "left" (Token-ID, 8149), an beiden Stellen des Satzes beispielsweise
eine unterschiedliche Bedeutung. Das erste Vorkommen bedeutet so viel wie "vergessen", während das zweite Vorkommnis auf eine Richtung hinweist.
Würde jeweils immer der selbe Einbettungs-Vektor pro Wort an das vortrainierten Transformer-Modell übergeben werden,
könnte das Modell keinen Unterschied in der Bedeutung feststellen. Aus diesem Grund muss musste ein Weg gefunden werden,
jedes Wort, abhängig von seiner Position im Text eindeutig und gleichzeitig voneinander unabhängig einzubetten.
Dieses Verfahren wird positionsbezogene Kodierung (Positional Encoding) genannt.
Ähnlich des Verfahrens zum Abruf der Einbettungs-Vektoren je Token-ID aus der Token-Einbettungs-Übersetzungs-Matrix,
wird beim Training des GPT-2-Modells eine Positions-Matrix trainiert, die für jede mögliche Position, einen eindeutigen
Vektor definiert, der nicht mit anderen Positionsvektoren verwechselt werden kann, die gleiche Dimensionalität hat und dessen Elemente
ebenfalls auf der Skala [-1..1] normalisiert sind. Jeder Positionsvektor wird also durch 768 Zahlen auf der Skala [-1..1] beschrieben.
Auch die Positions-Matrik stellt also eine Liste aus Vektoren dar. Die erste Zeile, also der erste Positions-Vektor
bezieht sich immer auf den ersten Token des Eingabetextes, die nachfolgenden Vektoren immer auf die jeweils nachfolgenden Token.
Diese Positions-Vektoren sind also statisch - sie sind für jede Eingabe immer die selben.
In dieser Positions-Matrix gibt es außerdem immer nur so viele Einträge, wie das Modell Tokens als Eingabe auf einmal verarbeiten kann (Maximum Input Tokens). Gibt der Tokenizer also mehr Tokens aus, als die Positions-Matrix Einträge enthält, wird bei der Verarbeitung der Eingabe ein Fehler geworfen werden (Maximum Length Error). Ist die Menge an Tokens kleiner oder gleich der Positions-Matrix, kann für jeden Token basierend auf seiner Position ein Positions-Vektor aus der Positions-Matrix abgerufen werden. In diesem Fall erhalten wir also eine Liste an Positions-Vektoren, die so lang ist wie die Anzahl der Tokens, die sich mittels des Tokenizers aus dem Eingabetext ergeben.
Um den ursprünglichen Einbettungs-Vektor, der noch nicht zwischen den selben Worten an unterschiedlichen Stellen unterscheiden kann, nun so anzureichen, sodass eine Unterscheidung der selben Worte und Zeichen, die an unterschiedlichen Stellen im Eingabetext vorkamen, möglich wird, wird jeder Einbettungs-Vektor mit dem zu seiner Position passenden Positions-Vektor addiert.
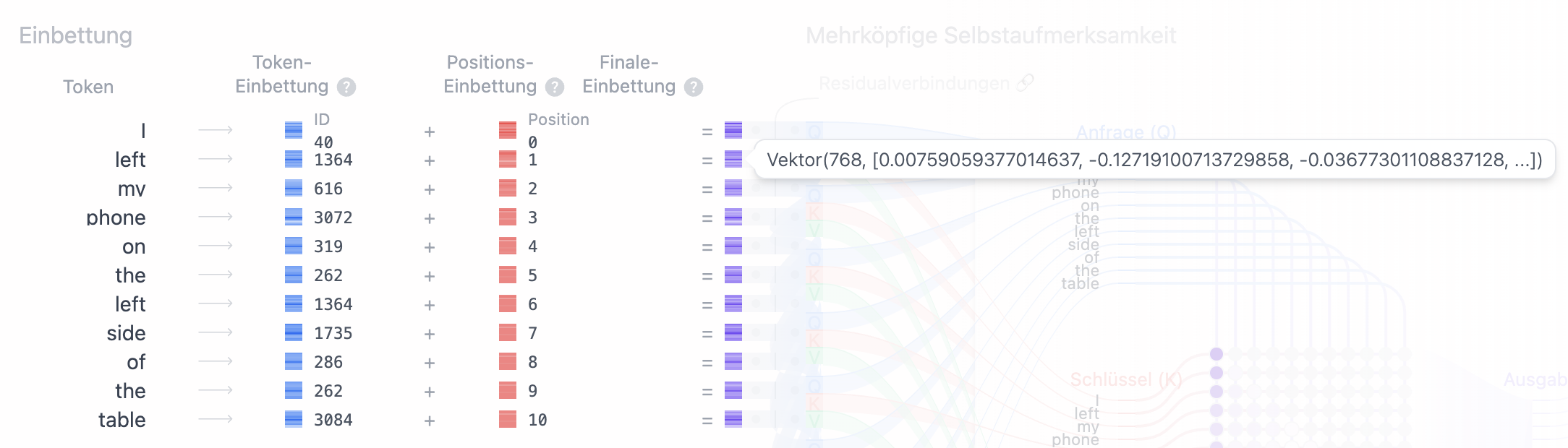
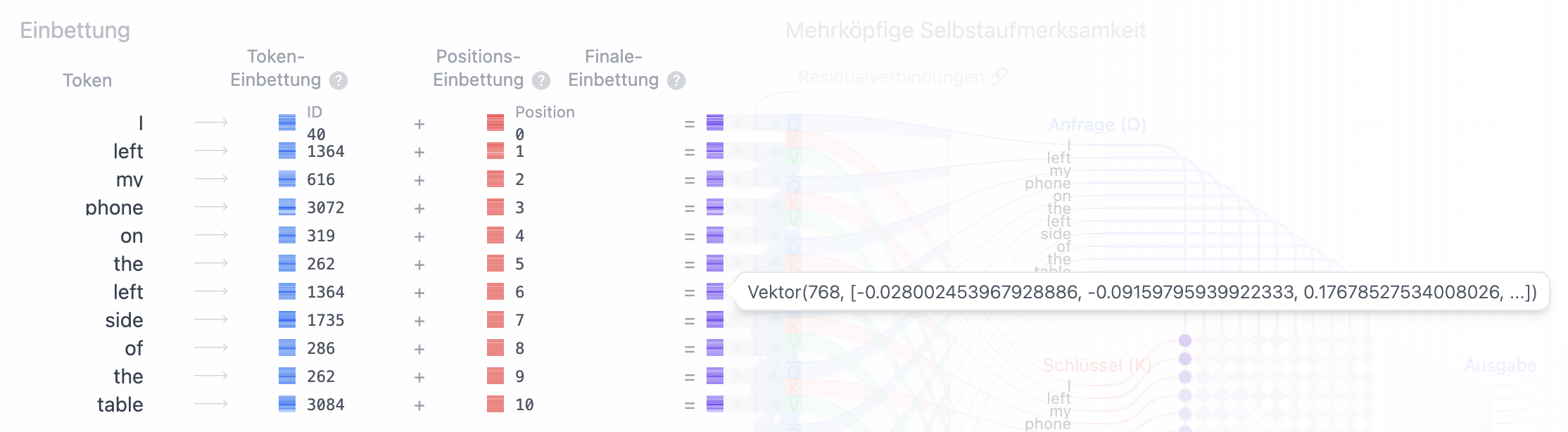
Führen wir hier nochmals den Token "left" an. Wie in Abb. 1 und Abb 2. zu erkennen ist, ergibt der Token an beiden jeweils den selben Einbettungs-Vektor,
jedoch ergibt sich, abhängig von seiner Position, ein unterschiedlicher Positions-Vektor (Abb. 3 und Abb. 4).
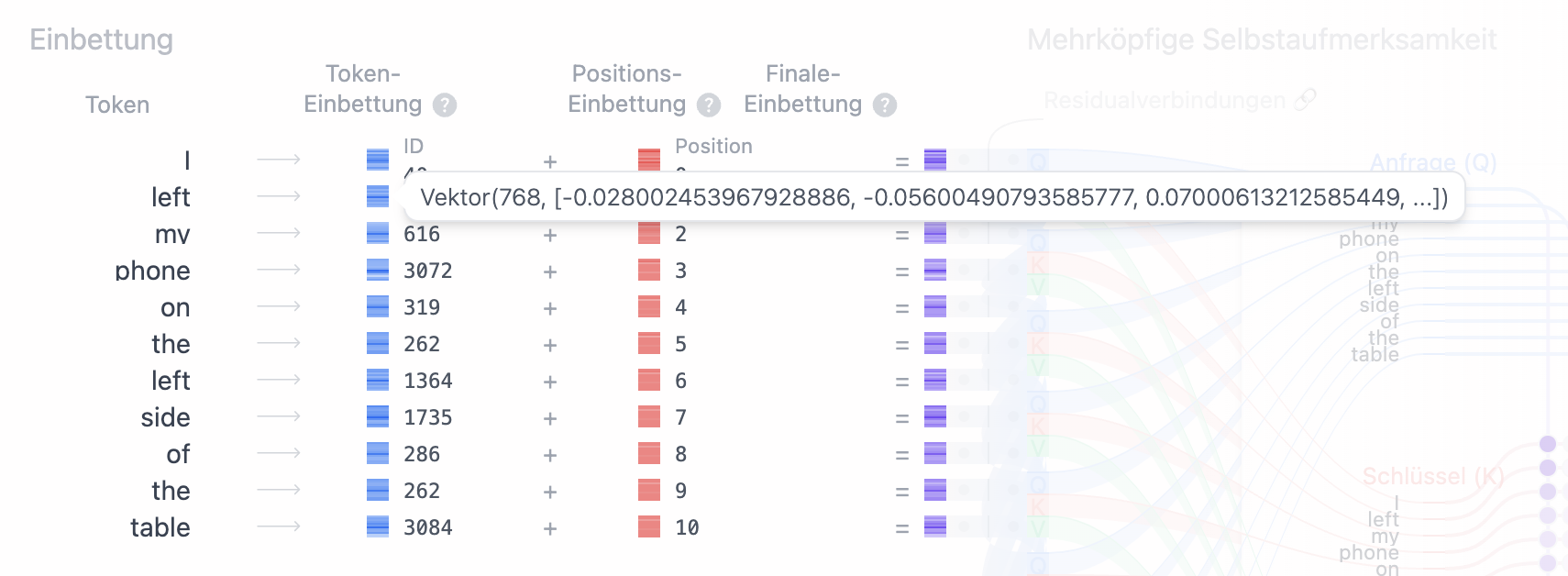
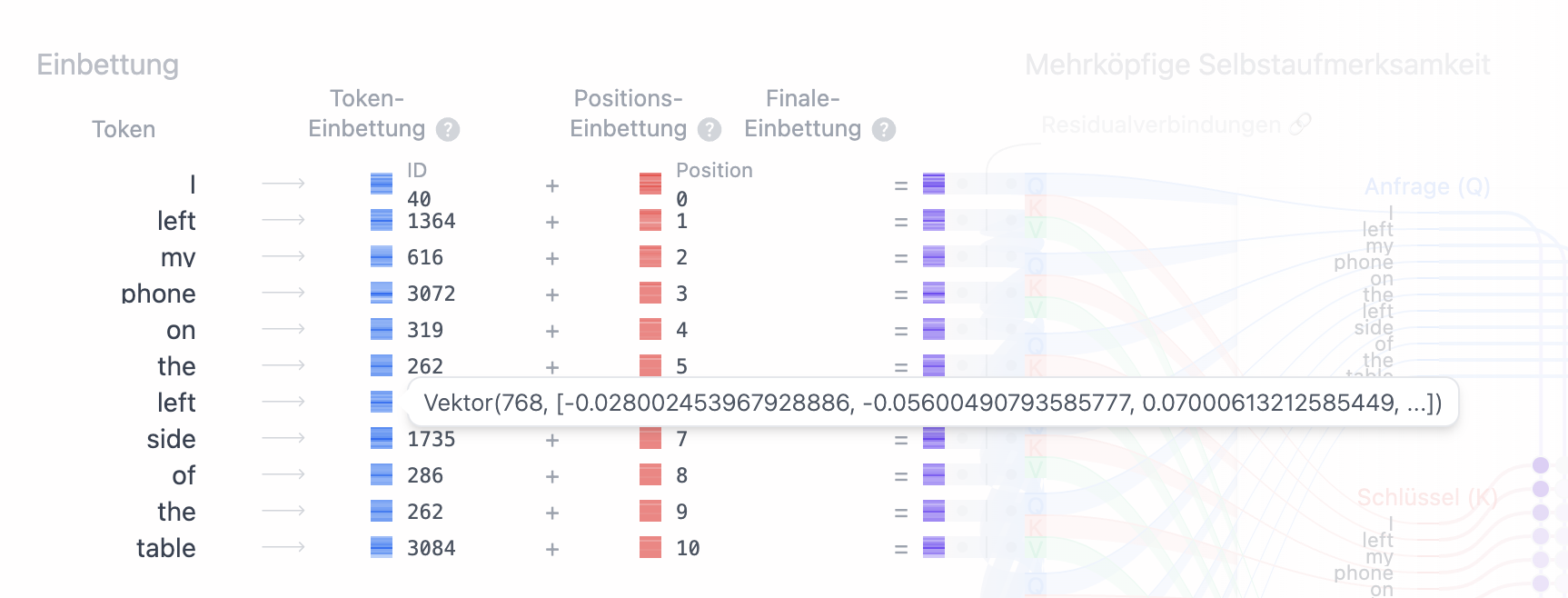
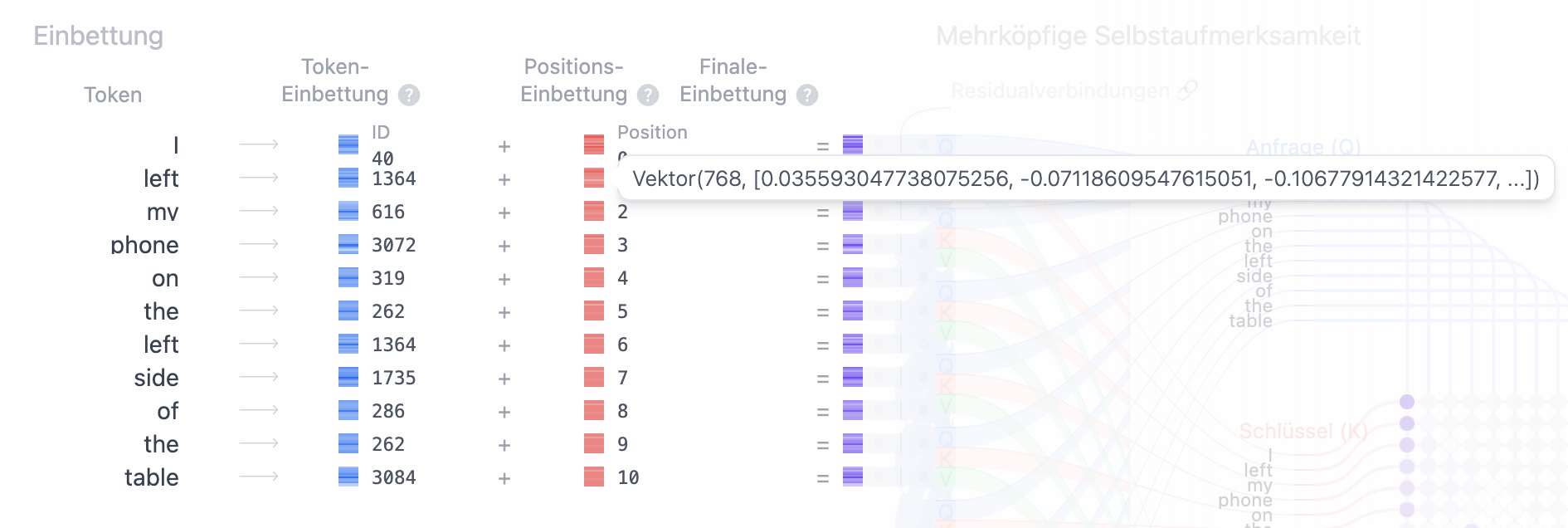
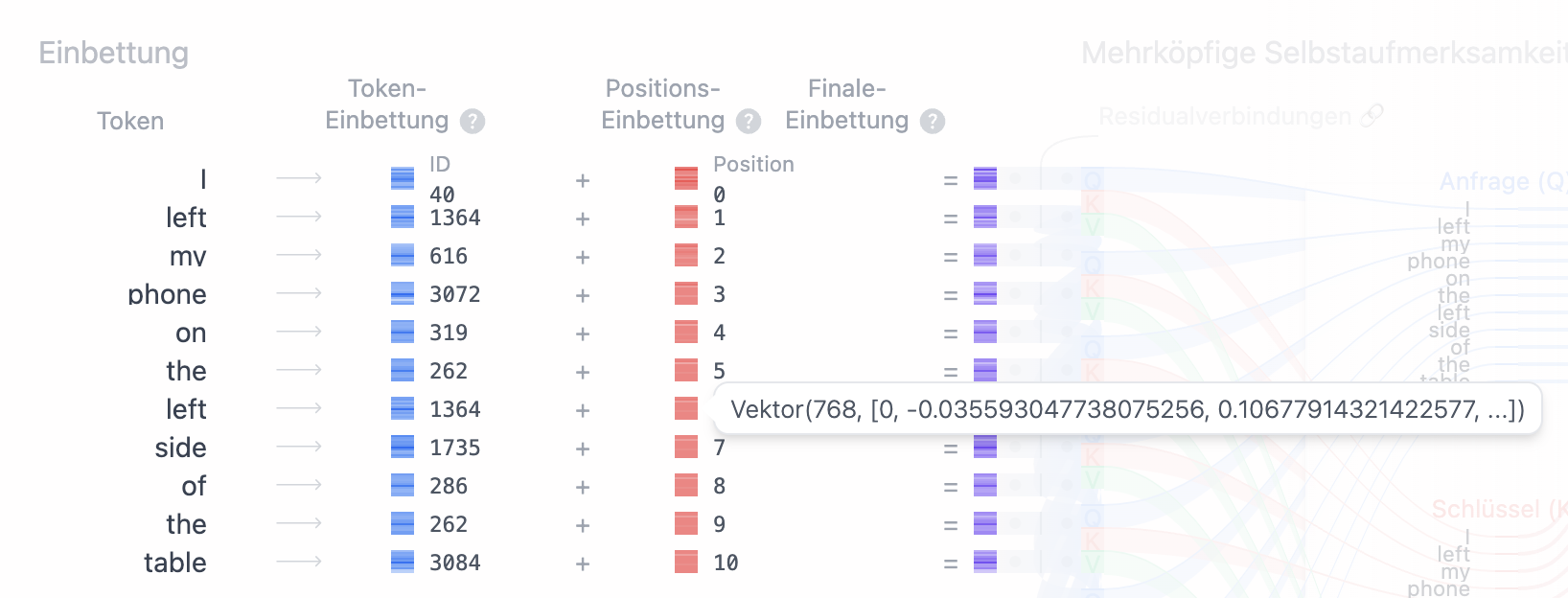
Nach der Vektor-Addition beider Vektoren (also der Addition jedes Elements im Einbettungs-Vektor mit jedem Element des Positions-Vektors), ergibt sich für jeden Token ein finaler Einbettungs-Vektor (Abb. 5 und Abb. 6):
Die finalen Einbettungs-Vektoren werden anschließend für die Verarbeitung im Modell (Inferenz) in den Speicher geladen.
Präzision: Eine Frage der Quantisierung
Nun haben wir aber noch ein letztes Problem: Wie soll denn der Abstand für jede Bedeutungsbeziehung überhaupt genau gemessen werden, wenn die Zahlen, die pro Bedeutungskategorie in den Vektor-Einbettungen verwendet werden, jeweils nur zwischen -1 und 1 liegen? Dieses Problem wird mit der Anzahl an Nachkommastellen gelöst - also der Präzision jeder Zahl. Denn ob wir nun schreiben: 0.1234 von 1 oder 1234 von 10000 - es ist der selbe relative Abstand, also die selbe Aussage einer Ratio, auch wenn die absolute Differenz unterschiedlich ist.
Das Ziel der Vektorisierung ist es, die semantische Bedeutung der Worte mathematisch beschreibbar und somit miteinander Vergleichbar machen. Aus diesem Grund betrachten wir nur die Ratio der Bedeutungen in Relation zueinander. Allerdings ist es durchaus wichtig, wie genau wir diese Abstände darstellen können. Wenn Sie sich nochmals die Zahlenstrahle ins Bewusstsein rufen, welche die Abstände pro Bedeutungskategorie kodieren, fällt Ihnen vielleicht auf, dass es je nach Bedeutungskategorie vielleicht gar nicht viele Werte gibt, die es zu kodieren gibt.
Wenn es nur 4 Kategorieren gäbe, brächte man auch nur 4 Zahlen, um diese voneinander unterscheiden zu können. Würden wir nur -1, -0.25, 0.25 und 1 speichern können, könnten wir bereits jede Kategorie eindeutig benennen. Wenn jedoch wenige Nachkommastellen genügen, um viele Bedeutungskategorien zu kodieren, warum sollten wir dann, wie bei typischen Gleitkommazahlen, 32 Bit pro Zahl speichern, also sehr viele Stellen nach dem Komma? Jede Nachkommastelle belegt, je nach Speichermethode, etwa 1 Bit im Speicher. Außerdem kann durch kleinere Speichermengen auch die Berechnung, also die Inferenz bei der Anwendung eines Modells effizienter umgesetzt werden. Diese Überlegung ist die Idee hinter dem Konzept der Quantisierung.
Genügen uns also beispielsweise bereits 4 Bit für eine hinreichend präzise Vorhersage der semantischen Bedeutung,
dann könnten wir im Modell doch gleich alle Zahlen einfach mit 4 Bit kodieren? Eine solche Quantisierung würde als quantisiertes Modell bezeichnet werden
(z.B. qint4 für eine Speicherung aller Zahlen, also aller Gewichte, Verzerrungen und Elemente von Vektor-Embeddings mit 4 Bit Ganzzahlen).
In der echten Welt kommt es bei der Quantisierung teilweise zur Verzerrung der semantischen Bedeutung, da nicht immer
sichergestellt werden kann, dass die semantische Bedeutung einer Zahl exakt mit einer geringen Anzahl an Bits kodiert werden kann.
Daher ergibt sich bei der Quantisierung von Modellen, abhängig von der gewählten Metrik, oft ein Trade-Off zwischen Speicher-/Rechenbedarf und Qualität von nur wenigen Prozentpunkten.
Menschen erkennen jedoch oftmals kaum einen Unterschied zwischen den Ergebnis quantisierter und nicht quantisierter Modelle.
Eine Quantisierung findet meist nach dem Training eines Modells statt, wurden also ursprünglich mit 32 Bit Gleitkommazahlen trainiert. Neuere Ansätze ermöglichen jedoch auch die Quantisierung bereits beim Training von Modellen. Quantisierung ist in den vergangenen Jahren immer populärer geworden. In den vergangenen Jahren wurde auch die Hardware, also oft GPUs und TPUs daraufhin weiterentwickelt, neue Instruktionen zu unterstützen, die die Ausführung von quantisierten Modellen beschleunigen, indem sie z.B. die Parallele Berechnung von 16 Bit und 4 Bit Ganzzahlen ermöglichen.
Unter anderem dadurch gelingt es heutzutage, oftmals quantisierte KI-Modelle auf dem eigenen Rechner, Laptop, Smartphone, Server und manchmal sogar direkt im Browser effizient und Datenschutz-konform (DSGVO/GDPR-kompatibel) auszuführen. Diese Website führt beispielsweise gerade das von mir als 4 Bit Ganzzahl (qint4) quantisierte KI-Modell GPT-2 in Ihrem Browser aus. Durch die Quantisierung ist das Modell auch nur etwa 167 MB anstatt von 656 MB groß. Zum Zeitpunkt der ursprünglichen Veröffentlichung von GPT-2 war die Quantisierung von KI-Modellen noch kein populäres Thema.
Aktuell kommen primär GPTQ und AWQ als Quantisierungsverfahren zum Einsatz. Letzteres Verfahren ist moderner uns besonders effizient.
Der Fluch der (Hoch-)Dimensionalität
Vielleicht haben Sie bereits bemerkt, dass ein Vektor mit 768 Dimensionen immer noch sehr viele Zahlen enthält. Selbst, wenn diese Zahlen quanisiert wären, also mit wenigen Nachkommastellen auskommen, müssten letztlich weiterhin bei jedem Vektor-Rechenschritt 768 Rechenoperationen durchgeführt werden. Da wir für die Vektorisierung jeden Token des Vokabulars in einem solchen Vektor abbilden müssen und auch für Training- und Inferenz des künstlichen neuronalen Netzes entsprechend viel Speicher- und Reaufwand entsteht, wird eine hohe Dimensionalität auch als Fluch bezeichnet (Curse of Dimensionality). Desto mehr Dimensionen die Vektoren haben, desto mehr Rechenleistung und Speicher wird benötigt, um die semantische Bedeutung der Worte zu verarbeiten.
Dimensions-Reduktion
Dieses Problem ist jedoch nicht unlösbar. Es gibt verschiedene Methoden, um die Dimensionalität von Vektoren zu reduzieren, ohne dabei die mathematische Beschreibung der Daten so stark einzugrenzen, dass sie nutzlos werden.
Die Idee hinter diesen Methoden ist es, dass unterschiedliche Anwendungsfälle, in denen z.B. ein Sprachmodell zum Einsatz kommt, jeweils nur eine ihrem Anwendungsfall entsprechend präzise Abbildung der Daten, also beispielsweise der Worte und Sätze benötigen. Ist es beispielsweise nur wichtig, die Sentiment-Analyse eines Textes durchzuführen, also zu erkennen, wie positiv oder negativ eine Aussage gemeint ist, so könnten vielleicht weniger als 768 Dimensionen ausreichen, um diese Aufgabe zu erfüllen.
Eine der Methoden, um die Dimensionalität schon beim Training eines Modells zu beeinflussen und später dynamisch wählen zu können, ist das so genannte "Matryoshka-Representations-Lernen". Matryoshka-Representations-Lernen wurde 2022 im gleichnamigen Paper "Matryoshka Representation Learning (MRL)" vorgestellt und hat seitdem viel Aufmerksamkeit in der KI-Forschung auf sich gezogen. Es ist ein Ansatz, der insbesondere bei Vektor-Einbettungsmodellen zum Einsatz kommt und seit Januar 2024 auch in OpenAI Embedding-Modellen verwendet wird.
MRL macht sich die Idee von Schachtelstrukturen zu nutze, die ähnlich wie die berühmten russischen Matroschka-Puppen funktionieren, bei denen kleinere Puppen in größeren verborgen werden. Vektorrepräsentationen werden dabei so strukturiert, dass die semantischen Informationen hierarchisch auf verschiedenen Ebenen gespeichert werden. So können z.B. äußeren Schichten, d.h. die ersten und letzten Elemente von Vektoren allgemeine, übergeordnete Bedeutungen beschreiben, während in den inneren Schichten spezifischere Details gespeichert werden.
Durch diese hierarchische Anordnung wird es möglich, die Dimensionen der Vektoren zu reduzieren, also Elemente einfach nicht zu ignorieren, und nicht in Berechnungen einzubeziehen, indem nur die relevanten Ebenen für eine bestimmte Aufgabe verwendet werden. Dies führt nicht nur zu einer effizienteren Nutzung der Rechenressourcen, sondern hilft teilweise auch, das Problem der Überanpassung zu minimieren, indem irrelevante oder redundante Informationen ausgefiltert werden.
Matryoshka-Representations-Lernen ist ein generalisierbarer Ansatz, der nicht nur bei der Vektorisierung von Texten, sondern auch bei anderen Arten von Daten, wie Bildern, Audio oder Zeitreihen, eingesetzt werden kann. Im Folgenden sehen Sie ein Beispiel Anhand von Fotos, in denen Objekte korrekt erkannt, also klassifiziert werden sollen. "GT" entspricht dabei der Ground Truth, also der korrekten Klassifizierung. Es lässt sich leicht erkennen, dass selbst bei einer geringen Dimensionalität viele Objekte noch korrekt erkannt werden können.
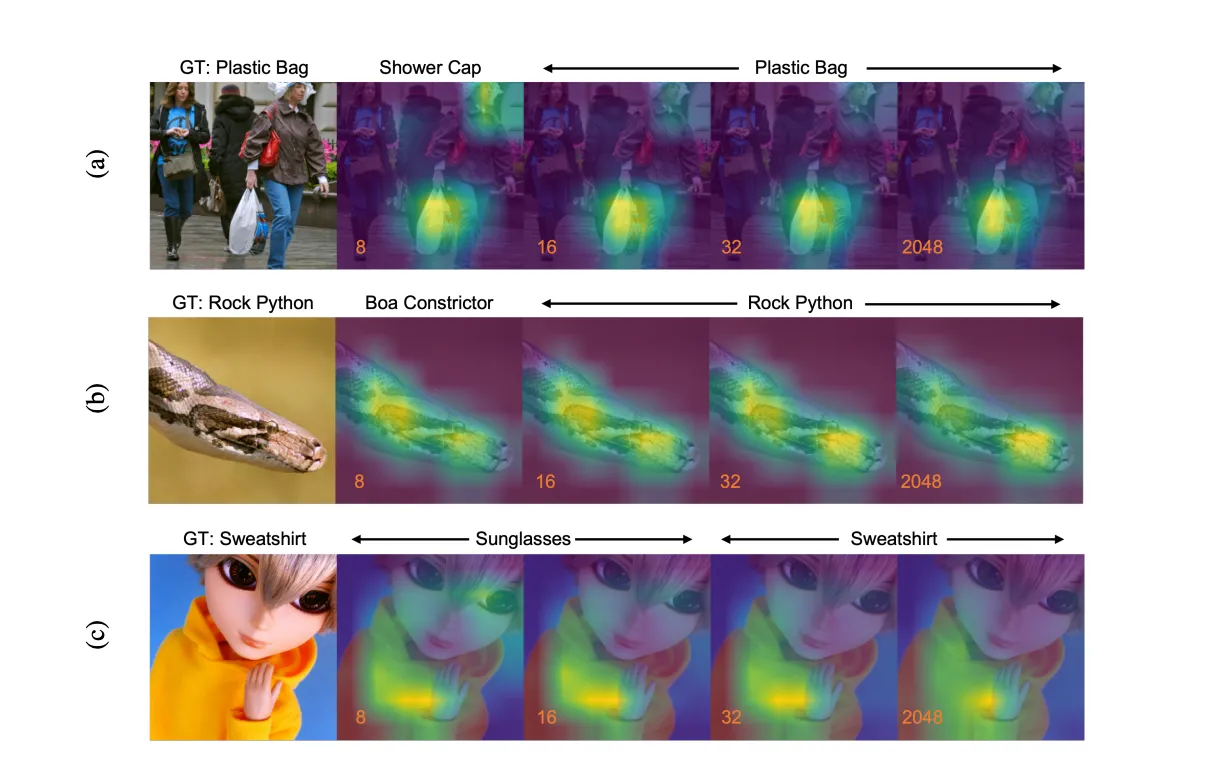
Matryoshka-Representations-Lernen kann auch bei der Modellinterpretation helfen, da es ermöglicht,
die verschiedenen Bedeutungsebenen separat zu analysieren und so ein besseres Verständnis der Strukturen in den Daten zu gewinnen.
Moderne, Transformer-basierte Vektor-Einbettungsmodelle wie die von OpenAI, Nomic, Cohere, und Deepset/Mixedbread setzen diese Methode bereits
erfolgreich produktiv ein. Der relevante Parameter in den API-Endpunkten, der die zu verwendene Dimensionalität angibt, heißt meist dimensionality.
Ethische und politische Implikationen: Trainingstexte führen zu Bedeutungshoheit
Lange Rede, kurzer Sinn: Für jede Token-ID haben wir nun einen Vektor mit 768 Dimensionen. Jedes Element, also jede Zahl in diesem Vektor, kodiert eine Bedeutungsbezuehung, also wie weit dieses Wort z.B. in der Bedeutung "Geschlecht" von allen anderen Termini im Vokabular entfernt ist. Die Skalen und Grenzwerte, also was "Geschlecht" bedeutet, werden beim Training ähnlich automatisch erlent, wie das Vokabular des Tokenizers. Wird also auf sehr viel Text trainiert, der sich nur auf zwei Geschlechter bezieht, wäre die Skala zwischen Frau und Mann definiert. Wird ein Modell auf Texte trainiert, dass auch andere Geschlechterdefinitionen beinhaltet, wird schon bei der Vektor-Einbettung eine semantische Bedeutungsabbildung jeden Wortes möglich, die z.B. auch andere Geschlechter bzw. Geschlechtsidentifikation mit einbezieht. Diese Funktionsweise ist sehr wichtig für die spätere Weiterverarbeitung im Sprachmodell und äußerst relevant für Sprachen mit generischem Maskulin.
Ähnliche Problemstellungen ergeben sich auch bei anderen, für eine Gesellschaft kritische semantischen Bedeutungsräume, wie z.B. "Herkunft", "Religion", "Politik", "Gesundheit" oder "Klima". Da große Sprachmodelle und deren Trainingsdaten oftmals nicht frei und kaum dokumentiert sind, ist es für die Öffentlichkeit und Forschung schwer nachzuvollziehen, wie sich diese Modelle verhalten würden und ob sie für den Betrieb sicher sind. Eine absolute Sicherheit kann nach aktuellem Forschungsstand nicht garantiert werden, da es sich bei Sprachmodellen um komplexe, nicht-deterministische Systeme handelt, und die Prozesse zur Absicherung der KI-Modelle weder standardisiert noch fehlerfrei durchzuführen sind und selbst kleine Änderungen in den Trainingsdaten zu unerwarteten Verhaltensweisen führen können. Da KI-Modelle stetig weitertrainiert werden, ist es auch nicht möglich, die semantische Bedeutung der Vektoren und damit eine Bedeutungshoheit zu fixieren, ohne dabei die Weiterentwicklung, also die Verbesserung der Modelle in den gleichen und anderen Bereichen zu behindern.
Wie werden Eingebettungs-Modelle trainiert?
Wie wir bereits gesehen haben, werden Trainingstexte durch einen Tokenizer und dessen vortrainiertes Vokabular in Token-IDs kodiert und als sortierte Liste ausgegeben. Um Einbettungsmodelle zu trainieren, bei denen Wörter (und Sätze), die eine ähnliche semantische Bedeutung haben, muss ein Weg gefunden werden, die semantische Bedeutung der Wörter und Zeichen untereinander in Beziehung zu setzen und diese Beziehungen mathematisch zu beschreiben. Die naheliegendste und effizienteste mathematische Darstellungsform für dieses Problem sind, wie bereits dargelegt wurde, hochdimensionale Vektoren. Durch diese hochdimensionalen Vektoren können Wörter, die semantisch ähnlich sind, in der Nähe zueinander im Vektorraum positioniert werden, was dem Modell hilft, Bedeutungen und Beziehungen zwischen Wörtern zu erfassen und zu verarbeiten. Projiziert man die Vektoren aus dem hochdimensionalen Raum zurück in eine farb-kodierte 2D-Darstellung, ergeben sich „Wolken“, die semantische Beziehungen abbilden.
Um jedoch zu einem solchen Ergebnis zu kommen, muss schrittweise vorgegangen werden. Im ersten Schritt wird festgelegt, wie viele semantische Dimensionen jeder Token zueinander abbilden kann. Für GPT-2 wurden hierfür 768 Dimensionen festgelegt.
Da die semantische Bedeutung der Wörter (Tokens) zueinander anfangs noch nicht bekannt ist, wird sie schlichtweg zufällig bestimmt. Der Vektor für die Token-ID 2902, "tea", die "Tee" bedeutet, zeigt also zunächst in einem 768-dimensionalen Raum in eine zufällige, hochdimensionale Richtung. Während des Trainings wird nun fortwährend die Häufigkeit der einzelnen Tokens im Trainingstext-Korpus zueinander gemessen. Die Nähe von Tokens zueinander wird auch als Kontext bezeichnet: „In welchem Kontext kommen Wörter häufig miteinander vor?“. Die Kontextlänge, also die Menge an Tokens, die einen Kontext beim Training ausmachen, bestimmt letztlich, wie gut die semantische Bedeutung ganzer Halbsätze, Sätze und Absätze von Texten in einem Vektorembedding erfasst werden kann.
Je mehr Wörter miteinander in Kontext gesetzt werden können, desto höher ist auch die semantische Informationsdichte der Vektoreinbettungen. „Komm, wir essen, Opa“ sollte eigentlich recht weit von „Komm, wir essen Opa“ entfernt sein. Würde ein Vektorembedding-Modell jedoch nur auf einzelne Worte trainiert wie ältere Modelle (z.B. Word2Vec), könnten solch subtile, aber bedeutsame semantische Bedeutungsunterschiede, logische Induktionsfehler in der Text-Genierung des Modells die Folge sein. Der hochdimensionale Raum, seine vielen Dimensionen, und damit einhergehend seine Bedeutungskategorien, machen hier den entscheidenden Unterschied in der Qualität der Beschreibung semantischer Beziehungen der Tokens untereinander und spielen folglich auch eine maßgebliche Rolle der Qualität der Fähigkeit der korrekten Generalisierung und Textausgabe des Modells.
Kommt die Token-ID 2902, "tea" für "Tee" im Trainingstext deutlich häufiger in der Nähe der Token-ID 286, "honey" für "Honig" vor, als das Wort „Ratte“ ("rat"), identifiziert durch die Token-ID 8229, werden die Vektoren dieser Token-IDs im euklidischen Raum beim Training schrittweise immer näher zueinander bewegt, während sich der Vektor für das Wort "Ratte" deutlich vom Vektor für „Honig“ und „Tee“ entfernt. Der Algorithmus, der hierfür zum Einsatz kommt, ist der stochastische Gradientenabstieg ("Stochastic Gradient Descent", SGD). Die Sinnhaftigkeit des Ergebnisses dieses Vorgangs hängt jedoch stark von der Bandbreite der Trainings-Textauswahl ab. Würde ein Einbettungsmodell allein auf einer einzigen fiktiven Geschichte von Ratten, die Honig mögen und mit Bienen befreundet sind basieren, hätten die Vektoren der genannten Wörter kaum einen Abstand zueinander. Das Vektorembedding-Modell könnte keine sinnvolle Generalisierung der Beziehungen der semantischen Bedeutung aller Worte aller Sprachen abbilden. Trotz großem Kontext und hoher Dimensionalität würde solch ein Vektor-Einbettungsmodell die semantische Bedeutung der Wörter zueinander völlig verzerrt darstellen.
Vektordatenbanken: Wie und wo können Vektor-Einbettungen verwendet werden?
Vektor-Einbettungsmodelle werden, wie große Sprachmodelle, in Abschnitten, gennant "Epochen", trainiert. Nach vielen Trainingsepochen ist das Vektor-Embedding-Modell schließlich soweit auftrainiert, dass es die semantischen Beziehungen zwischen den Wörtern gut repräsentiert. Ein Qualitätsmerkmal vieler Vektor-Einbettungsmodelle ist die Kuratierung von Textdaten unterschiedlicher Sprachen, Themenbezüge und sogar Kodierungen. Beispielsweise werden die Vektor-Einbettungsmodelle, die im Zusammehang mit großen Sprachmodellen trainiert werden, auch mit z.B. Base64-kodierten Inhalten trainiert. Auf diese Weise ist es möglich, dass das Sprachmodell auch über kodierte Eingangstexte generalisieren kann.
Enthielt das Trainingsdatenset des Modells auch Übersetzungstexte und Texte in mehreren Sprachen, kann ein einzelnes Vektor-Embedding-Modell auch die semantische Bedeutung von mehrsprachigem Text erfassen. Die Vektoren, die aus der Kodierung von Text mittels eines Vektor-Embedding-Modells resultieren, können entweder in Verbindung mit einem Sprachmodell und Positionskodierung (Positional Encoding) verwendet werden, um möglichst sinnvolle Vorhersagen für Antworttexte zu generieren, oder sie können in Vektordatenbanken indexiert werden, um im Nachhinein eine Suche nach Texten mit ähnlicher Bedeutung zu ermöglichen – sogar wenn der Text in einer anderen Sprache verfasst wurde. In der Regel sind, wie eingangs erwähnt, beide Einsatzgebiete miteinander verbunden, Modelle werden jedoch oft auf spezifische Einsatzgebiete hin optimiert und sind untereinander nicht austauschbar. Die Vektor-Einbettungen des Nomic Text Embed V1-Modells können also nicht einfach in einem Sprachmodell verwendet werden.
Vortraining eines GPT-Sprachmodells
Nachdem der Tokenizer und das Vektor-Einbettungsmodell trainiert wurde, sowie die Positions-Matrix und die Token-Einbettungs-Übersetzungs-Matrix erstellt wurden, ist das Ziel des Vortrainings zunächst, dem Sprachmodell ein allgemeines Verständnis von Sprache zu vermitteln (Generalisierung). Mittels dieses Vorgangs ist es in der Lage, Texte zu vervollständigen, Fragen zu beantworten oder neue Sätze zu generieren. Um dieser Aufgabe nachzukommen, ist eine andere mathematische Grundlage von Nöten: Das neuronale Netz und Aufmerksamkeitsmechanismen.
Es ist zunächst wichtig zu verstehen, dass neuronale Netze und Neuronen in KI-Modellen nicht der Struktur der Neuronen des menschlichen Gehirns ähneln. Die Idee von neuronalen Netzen entstammt einem sehr stark vereinfachten Modell des menschlichen Gehirns, das in den 1940er Jahren von Warren McCulloch, einem Neurophysiologen, und Walter Pitts, einem Logiker, aufgebracht wurde. Sie veröffentlichten 1943 ein wegweisendes Paper mit dem Titel "A Logical Calculus of Ideas Immanent in Nervous Activity". Ihr Modell, bekannt als das McCulloch-Pitts-Neuron, war eine stark vereinfachte mathematische Darstellung eines Neurons, das entweder aktiviert wird (also eine 1 ausgibt) oder nicht aktiviert wird (also eine 0 ausgibt). Eine Vernetzung von solchen künstlichen Neuronen ermöglicht die Abbildung komplexer, hochdimensionaler Muster in Daten.
Stellen Sie sich dazu vor, dass wir bedingte Wahrscheinlichkeiten abbilden möchten. Immer wenn die Sonne scheint, geht der Sprinkler im Garten an. Wenn es regnet, geht der Sprinkler aus. Diese Logik könnte bereits mit wenigen künstlichen Neuronen abgebildet werden. Eine 1 bedeutet "aktiviert", eine 0 bedeutet "nicht aktiviert". Stellt man sich nun vor, dass jedes Neuron eine Bedingung abbildet, die in der Natur vorkommt, können wir mit einem künstlichen neuronalen Netz so ziemlich jede logische Verknüpfung abbilden, die wir uns vorstellen können. Um die Eintrittswahrscheinlichkeiten genauer bestimmen zu können, legen wir auf die Verbindungen zwischen den künstlichen Neuronen noch numerische Gewichte und Verzerrungen (dazu später mehr). Denn wenn die Sonne sehr stark scheint, könnte der Sprinkler auch bei leichtem Regen anbleiben. Wenn ein Baum umfällt, könnte der Schatten den Sprinkler auch ausschalten und die eigentliche Regel außer Kraft setzen - also verzerren. Bitte verstehen Sie diese Beschreibung als die pseudo-wissenschaftliche Metapher, die sie ist. Sie gilt vor allem als mentales Erklärungsmodell der deutlich komplexeren Abläufe, die tatsächlich in großen Sprachmodellen ablaufen.
Das Ziel des Trainingsprozesses eines großen Sprachmodells ist es, aus den semantischen Beziehungen der Wörter und Sätze, die bereits in den Vektoren kodiert sind, sehr viele künstliche Neuronen zu erstellen und in Schichten miteinander zu vernetzen, um so die semantischen Beziehungen der Wörter und Sätze zu generalisieren. Wird anschließend ein Eingabetext in das Modell eingegeben, versucht das Modell sich schrittweise an die Muster der Trainingsdaten anzupassen, um so eine Vorhersage zu treffen, was als nächstes Wort oder welcher Satzteil semantisch korrekt folgen könnte. Ein solches Modell wird als "Sprachmodell" bezeichnet und könnte mathematisch auch als Funktions-Approximator verstanden werden, da es lediglich versucht, die semantischen Beziehungen der Wörter und Sätze in den Trainingsdaten zu approximieren.
Trainiert man ein solches künstliches neuronales Netz, wird das Netz durch einen Prozess optimiert, bei dem die Gewichte und Biases der Neuronen schrittweise angepasst werden. Dieser Prozess, bekannt als Backpropagation, beginnt damit, dass das Netzwerk eine Vorhersage basierend auf den Eingabedaten macht. Diese Vorhersage wird dann mit dem tatsächlichen Ergebnis verglichen, um den Fehlerwert zu berechnen. Der Fehlerwert wird mittels einer Metrik ermittelt. GPT-2 verwendet hierfür Cross-Entropy Loss. Diese Metrik misst, wie gut die vom Modell vorhergesagten Wahrscheinlichkeiten für die nächsten Token mit den tatsächlichen Token im Text übereinstimmen.
Der Fehler wird anschließend rückwärts durch das Netzwerk propagiert (von der Ausgabeschicht zur Eingabeschicht hin), um festzustellen, wie stark jeder einzelne Parameter (Gewicht, Bias) zu diesem Fehler beigetragen hat. Basierend auf dieser Information werden die Parameter so angepasst, dass der Fehler bei zukünftigen Vorhersagen verringert wird. Durch viele Wiederholungen dieses Prozesses (in so genannten "Epochen") lernt das neuronale Netz, immer präzisere Vorhersagen zu treffen. Im Laufe des Trainings passt es sich also immer besser an die zugrunde liegenden semantischen Muster in den Textdaten an, was zu einer verbesserten Leistung bei Aufgaben wie der Textvorhersage, also der Generierung (das G in "GPT", steht für "generativ") von Text führt.
Das Ergebnis des Vortrainings ist ein Modell dass oft als "Pretrained" bezeichnet wird (das P in GPT). Vortrainiere Sprachmodelle sind noch nicht auf spezielle Anwendungen wie das Chatten optimiert. Sie generalisieren lediglich bereits einigermaßen gut - das bedeutet, dass sie nicht allein die Texte wiedergeben können, die sie gelernt haben, sondern Texte im Muster der Sprache und der gelernten Inhalte wiedergeben können - auch in einer Art und Weise, auf die sie zuvor nicht speziell trainiert wurden.
Auch Instruktionen, wie sie beim Prompt Engineering erstellt werden, befolgen Sprachmodelle, die noch keine Feinabstimmung (Fine-Tuning) durchlaufen haben, meist noch nicht sonderlich gut.
Feinabstimmung (Fine-Tuning)
TODO: Stochastic Gradient Descent erklären
Normalisierung pro Schicht
Die Layer-Normalisierung in GPT-2 passt die Eingabevektoren jeder Schicht so an, dass sie eine einheitliche Verteilung haben. Das bedeutet, dass die Werte innerhalb eines Vektors so standardisiert werden, dass sie denselben Durchschnitt (Mittelwert) und dieselbe Streuung (Varianz) aufweisen. Diese Standardisierung sorgt dafür, dass GPT-2 gleichmäßiger lernt und nicht so stark von den anfänglichen Werten der Gewichte abhängt.
Schauen wir uns das einmal anhand zweier Beispiele an:
- Nicht-normalisierte Eingabewerte: Angenommen, die Werte innerhalb eines Vektors
in einer Schicht, beispielsweise im MLP, reichen von sehr kleinen Werten wie 0,1 bis zu sehr großen Werten wie 100:
[0.1, 4.674, 78, 30, 99.9]. Diese breite Streuung kann dazu führen, dass das Modell Schwierigkeiten hat, die richtigen Beziehungen zwischen den Werten zu lernen. Ohne Normalisierung könnte das Modell sich zu stark auf die großen Werte konzentrieren und die kleineren ignorieren. - Normalisierte Eingabewerte: Durch die Layer-Normalisierung in GPT-2 werden diese Eingabewerte so angepasst,
dass sie beispielsweise alle zwischen
-1und1liegen. Dadurch wird sichergestellt, dass die Eingaben gleichmäßig verteilt sind. Die Normalisierung sorgt dafür, dass das Modell die Beziehungen zwischen den Werten besser lernen kann, weil alle Werte relativ zueinander konsistent sind. Zudem eröffnet die Normalisierung auch Optimierungsmöglichkeiten, da der Zahlenraum klar definiert ist.
In GPT-2 wird die Layer-Normalisierung in jedem Transformer-Block zweimal eingesetzt: einmal vor dem Selbstaufmerksamkeits-Mechanismus und einmal vor der MLP-Schicht. Diese Normalisierung trägt dazu bei, dass das Modell stabil lernt, weil es richtig auf unterschiedliche Eingaben reagieren kann.
Ohne eine Normalisierung würde sich in jeder Trainingsepoche die Verteilung der Eingabewerte ändern, was dazu führen könnte, dass das Modell nicht konvergiert. Das bedeutet, dass das Modell weder effizient lernt noch generalisiert, und die Metriken, die den Lernerfolg messen, würden keine eindeutige Verbesserung zeigen. Das Modell würde sich in diesem Fall beim Training nicht stabilisieren.
Auch bei der Inferenz ist die Normalisierung der Eingabevektoren wichtig, damit das Modell die richtigen Beziehungen zwischen den Werten erkennen kann. Die Layer-Normalisierung ist daher ein essenzieller Bestandteil von GPT-2 und eine wichtige Voraussetzung für sinnvolle Ergebnisse. Diese Notwendigkeit gilt nicht nur für GPT-Modelle, sondern für fast alle neuronalen Netzwerk-Architekturen (KI-Modelle).
Typische Probleme beim Lernprozess: Über- und Unteranpassung
Man könnte meinen, dass besseres Training bedeutet, dass man einem Sprachmodell lediglich so lange mehr Textdaten zum Training liefert, bis es eine perfekte Vorhersage über die nächsten Tokens treffen kann. Dem ist jedoch nicht so - der Effekt eines solchen Versuchs wäre eine "zu gute" Anpassung - die gefürchtete Überanpassung ("Overfitting"). In diesem Fall wäre das Modell so stark auf seine Trainingstexte optimiert, dass es häufig mit exakten Textteilen antworten würde, die in seinem Trainings-Textkorpus vorkommen, anstatt deren semantische Bedeutung zu generalisieren.
Das Gegenteil einer Überanpassung, also des Overfitting ist das Underfitting. Beim Underfitting handelt es sich um eine Situation, bei der dem Modell nicht genügend Trainingsdaten zu einem Thema vorliegen, um sinnvolle Vorhersagen zu treffen. Dies kann vorkommen, wenn entweder die für eine sinnvolle Antwort benötigten Trainingsdaten niemals vorlagen oder wenn das Modell zu wenige Neuronen oder Schichten enthält, um die Trainingsdaten sinnvoll zu vernetzen.
Dropout: Overfitting vermeiden
Um Überanpassung zu vermeiden, kommt bei GPT-2 eine statistische Methode zum Einsatz, die sich "Dropout" nennt: Dropout ist ein Verfahren, bei dem in jeder Trainingsepoche zufällig ausgewählte Neuronen in den versteckten Schichten des neuronalen Netzes deaktiviert werden. Sie können dies visuell inspizieren, indem Sie im Diagramm mit der Maus zwischen den Residualverbindungen und den finalen Vektor-Einbettungen hovern. Künstliche Neuronen, die zufällig deaktiviert sind, werden schlichtweg beim Lernprozess, also der Bestimmung der Gewichte und Verzerrrungen, nicht berücksichtigt. Dies zwingt das Modell, nicht zu stark von einzelnen Neuronen abhängig zu sein und stattdessen robustere, generalisierte Merkmale zu lernen.
Durch die Anwendung von Dropout lernt das Modell auch, die Informationen breiter über das Netzwerk zu verteilen, was die Fähigkeit verbessert, auch für neue, bisher ungesehene Eingabetexte, also Tokens, die so nicht in den Trainingsdaten vorkamen, gute Vorhersagen zu treffen. Die Zufallskomponente verhindert, dass das Modell dazu neigt, einfach die spezifischen Muster der Trainingsdaten auswendig zu lernen.
Residualverbindungen: Abkürzungen, die das Lernen verbessern
Residual-Verbindungen wurden erstmals 2015 im ResNet-Modell eingeführt und im gleichnamigen Paper vorgestellt. Diese Innovation revolutionierte das Deep Learning, indem sie das Training sehr tiefer neuronaler Netzwerke ermöglichte, ohne dass auf den langen Wegen zwischen den Schichten die Informationen so stark abgeschwächt werden, dass sie am Ende kein sinnvolles Ergebnis mehr liefern. Man kann sich das so vorstellen, wie wenn ein Mensch lange ins Grübeln gerät und am Ende nicht mehr weiß, was er eigentlich sagen wollte.
In der Mathematik spricht man bei der Analyse von Steigungen in Kurven von sogenannten Gradienten. Diese Gradienten werden während des Trainings eines neuronalen Netzes gemessen und verglichen, um die Parameter (also die Gewichte) zu optimieren. Die Gradienten geben die Richtung an, in der die Modellparameter angepasst werden sollten, um den Fehler zu minimieren (siehe Abschnitt "Stochastischer Gradientenabfall (SGD)"). Werden die Gradienten, also die Steigungen zu klein, verlieren sie an Aussagekraft und das Modell kann nicht mehr effektiv lernen.
Residualverbindungen lösen dieses Problem, indem sie die ursprünglichen Eingabewerte einer Schicht direkt zum Ausgang dieser Schicht hinzufügen, wodurch sie im nächsten Schritt wieder Teil der Eingabe werden. Die ursprüngliche Information bleibt dadurch erhalten, und die Gradienten flachen während des Trainings nicht so stark ab. Das Modell lernt so effektiver und kann mit tieferer Vernetzung und mehr Schichten trainiert werden.
Residualverbindungen kommen auch bei der Inferenz, also der Vorhersage bzw. der Generierung von Texten, zum Einsatz, um sicherzustellen, dass die Informationen auf dieselbe Weise verarbeitet werden wie beim Training.
Im Wesentlichen sind Residual-Verbindungen also Abkürzungen, die eine oder mehrere Schichten umgehen, indem sie den Eingang einer Schicht zu deren Ausgang hinzufügen. In der GPT-2-Modell-Architektur kommen Residual-Verbindungen zweimal vor: einmal zwischen der Eingabeschicht, also direkt nach der Vektorisierung der Eingabedaten, und dem MLP-Block sowie einmal innerhalb des MLP-Netzes. Im Falle von GPT-2 ermöglichen die Residialverbunden eine sinnvolle Generalisierung der semantischen Beziehungen der Eingabetexte.
Spezialisierung eines Sprachmodells als Chat-Modell
Nach dem Vortraining wird ein GPT-Modell in der Regel mit spezialisierten Daten weitertrainiert. Im Falle von GPT-Modellen, die als Chat-Modelle zur direkten Benutzerinteraktion ausgelegt sind, wie z.B. GPT-3, GPT-3.5, GPT-4, etc. bestehen diese Trainingsdatensätze meist aus realen oder simulierten Dialogen. Oft kommen auch spezielle Tokens zum Einsatz, die den Beginn und das Ende von Fragen, Antworten, und anderen Dialogelementen eindeutig zu kennzeichnen. Diese Daten können z.B. aus Kundenservice-Chats, Foren, transkribierten Gesprächen oder speziell erstellten Dialogszenarien stammen. Je mehr echte Daten ein KI-Modellanbieter zusammentragen kann und desto besser er diese Daten aufbereiten kann, desto höher ist die Wahrscheinlichkeit, dass sich das resultierende, chat-optimierte GPT-Modell in einem Dialog-Setting wie gewünscht verhält. Ein völlig deterministisches, korrektes Verhalten ist nach aktuellem Forschungsstand jedoch stets methodisch ausgeschlossen, da es sich bei großen Sprachmodellen nach der Transformer-Architektur um stochastische Systeme handelt. Aus statistischer Sicht handelt es sich um Sampling von mit hoher Wahrscheinlichkeit durch menschliche Intelligenz geprägten Textdaten. Aus philosophischer Perspektive würde man das Verhalten von LLMs vermutlich am besten als einen blinden, induktiven Schlussfolgerungsversuch betrachten.
„Verhalten“ ist hier grundsätzlich ein eher unpräzises Wort, da mit Verhalten gemeinhin eine Art Bewusstsein assoziiert wird. Diese liegt nicht vor. Ziel ist es lediglich, dem Modell die statistischen Wahrscheinlichkeiten in einer generalisierten Form anzutrainieren, die dazu führen, dass ein Mensch die vorhergesagten Antworttexte auf Eingaben als sinnvoll und kontextuell angemessen beurteilt. Eine echte künstliche Intelligenz (AGI) findet bei der Vorhersage von Text auf Basis von statistischen Wahrscheinlichkeiten und Generalisierungen in heutigen Transformer-Modellen nicht statt. Die Ausgabe von großen Sprachmodellen kann jedoch aufgrund ihrer Eigenschaften, leicht mit intelligenten Schlussfolgerungen verwechselt werden. Hierbei handelt es sich jedoch um einen Beurteilungsfehler, der lediglich aufzeigt, wie leicht es Menschen fällt, Korrelation mit Kausalität zu verwechseln.
Verstärkendes Lernen durch menschliches Feedback
Beim Verfahren des verstärkenden Lernens durch menschliches Feedback, kurz RLHF (Reinforcement Learning, Human Feedback) wird das Modellverhalten ferner durch die Integration von menschlichem Feedback verbessert. Diese Methode kam bei GPT-2 nicht zum Einsatz, ist jedoch Teil des Trainings aller moderner Sprachmodelle seit GPT-3.
Der Ansatz kombiniert traditionelle maschinelle Lernmethoden mit menschlichen Bewertungen und läuft folgendermaßen ab:
- Menschliche Akteuere, typischerweise so genannte "Domain Experts", also Personen, die in bestimmten Fachbereichen nachweislich Fachkenntnisse aufweisen, Verwenden das Sprachmodell, um Textantworten zu generieren. Diese Antworten werden anschließend mit positiven und negativen Bewertungen gelabelt. Ggf. kommen auch weitere Skalen-Bewetungen zum Einsatz wie z.B. ein Scoring der Genauigkeit, der Relevanz, Toxizität usw. Oft werden auch gleich mehrere Antworten generiert, um ein Ranking der Antwortqualität relativ zueinander zu ermöglichen. Darüber hinaus können teilweise auch gleich verbesserte Antworten vom Domain Expert vorgeschlagen werden. Auf diese Weise können aus den Feedbacks auch direkt neue Trainingsdaten generiert werden, welche beim Fine-tuning des Modells oder bei der Erstellung von neuen Modellen zum Einsatz kommen können.
- Auf Basis des Rankings der Antwortqualität können mit statistischen Methoden Belohnungsmodelle (Reward Models) trainiert werden. Diese integrieren über Scoring-Methoden die Bewertungen vieler Domain Experts, sodass ein Modell entsteht, das bei der Policy-Optimierung sinnvoll zum Einsatz kommen kann. Wichtig bei der Erstellung von Belohnungsmodellen ist, dass die Bewertungen der Domain Experts mit den statistischen Methoden korreliert werden können. Dies ist oft eine Herausforderung, da menschliche Bewertungen oft subjektiv sind. Aus diesem Grund benötigt es oft viele Domain Experts, um ein konsistentes Belohnungsmodell zu erstellen. OpenAI nutzt seit der Veröffentlichung von ChatGPT unter Anderem auch die Bewertungen der Nutzer*innen, um die Antwortqualität des Modells zu verbessern. Diese kommen in Form von "Likes" und "Dislikes", als auch in Form von Rerankings (also der Auswahl einer jeweils besseren Antwort) zum Einsatz.
- Bei der nachfolgenden Policy-Optimierung, also der Anpassung der Modellparameter, genauer gesagt der Gewichte und Verzerrungen der Neuronen, wird das Belohnungsmodell als Metrik in den Trainingsprozess integriert. Dies wird beispielsweise mit Methoden wie Proximal Policy Optimization (PPO) realisiert. Diese Methode wurde von OpenAI entwickelt und ermöglichen es, das Modell effektiv so zu trainieren, dass es die Wahrscheinlichkeit der Generierung von hochbewerteten Antworten erhöht wird. PPO verwendet dabei einen Clipping-Mechanismus, der extreme Änderungen in der Policy verhindert und so zu einer stabileren und graduellen Anpassung der Modellparameter führt. Weiterhin wird im Rahmen von PPO der Vorteil jeder Antwort geschätzt, um festzustellen, wie viel besser oder schlechter sie im Vergleich zu einer durchschnittlichen Antwort ist. Diese Vorteilsschätzung hilft dabei, die Trainingsrichtung gezielt zu steuern und effektiver auf das gewünschte Ergebnis hinzuarbeiten. Dennoch ist die Methode zeit-, ressourcen- und kostenintensiv, sowohl in menschlicher als auch in technischer Hinsicht.
- Eine modernere und vereinfachte Alternative zur konventionellen PPO stellt die DPO (Direct Preference Optimization)-Methode, zu Deutsch: Direkte Präferenz-Optimierung, dar. Ähnlich wie bei der PPO-Methode werden zuerst, wie im Schritt 1, menschliche Bewertungen gesammelt. Dieses begrenzt sich jedoch auf die Bewertungskategorien positiv (1) und negativ (0). Diese werden jedoch nicht in ein dediziertes, komplexes Belohnungsmodell überführt, sondern fließen in einem Trainingsschritt direkt durch Anpassung der Gewichte und Verzerrungen in die Modellparameter ein, indem KL-Divergenz oder neuderdings Binary Classifier eingesetzt werden, um zu berechnen, welche der vom Sprachmodell vorgeschlagenen Antwortoptionen die bessere wäre und entsprechend rückwirkend die Modellparameter der künstlichen Neuronen so anpasst, dass die Wahrscheinlichkeit erhöht wird, dass Sequenzen von Tokens generiert werden, die insgesamt eine qualitativ höhere, also von den Domain Experts bevorzugte Antwort ergeben würden.
Dieses Feedback wird genutzt, um das Modell so anzupassen, dass es Antworten generiert, die nicht nur technisch korrekt, sondern auch kontextuell angemessen und ethisch vertretbar sind. Ein zentraler Aspekt des RLHF ist, dass es kontinuierlich durchgeführt wird, wodurch das Modell ständig an die sich ändernden Anforderungen und Erwartungen der Benutzer angepasst wird. Diese Methode trägt dazu bei, die Relevanz und die Benutzerfreundlichkeit der Modellausgaben zu erhöhen und gleichzeitig unerwünschte Verzerrungen zu minimieren.
Über Halluzinationen, Induktion und Deduktion
Im Ergebnis, also bei der Anwendung des Modells, der Inferenz, entsteht aus dem Mangel an Information eine Halluzination. Dadurch, dass die Vernetzung der relevanten künstlichen Neuronen fehlt oder die Gewichte und Verzerrungen falsch gesetzt sind, kommt es bei der Vorhersage des nächsten Tokens zu einem Fehler, der dazu führt, dass ein beliebiges, sinnloses Wort oder Zeichen ausgegeben wird, da dieses als am wahrscheinlichen angesehen wird. An dieser Stelle sollten wir uns ins Bewusstsein rufen, dass große Sprachmodelle ihre Ausgabe nicht deduktiv hinterfragen können.
Die Generierung von Texten durch große Sprachmodelle basiert rein auf komplexen statistischen Modellen und der induktiven Methode. Damit unterliegt jeder generierte Text dem Induktionsproblem (vergl. Popper, Hume). Im Vergleich dazu ist es dem Menschen möglich, Schlussfolgerungen logisch-deduktiv und mithilfe der wissenschaftlichen Methode zu hinterfragen.
Exkurs: NVidia, Wirtschaftlichkeit und Klimaschutz
Mathematisch lassen sich solche Datenmengen übrigens sehr gut mittels Vektoren und Matritzen beschreiben. Vektoren und Matritzen werden auch bei der Beschreibung und Berechnung von 3D-Grafik benötigt. Matritzen-basierte Berechnungen sind jedoch vergleichsweise rechenaufwending, da oft viele Einzelrechnungen (z.B. Multiplikationen und Additionen) notwendig sind, um zu einem Gesamtergebnis zu kommen. Seit einigen Jahrzehnten haben sich Hersteller wie NVidia darum bereits darauf konzentriert, so genannte Grafikkarten, also Rechen-Beschleeunigerkarten zu produzieren, die es ermöglichen, solche Matritzen-Berechnungen besonders schnell und parallel auszuführen.
Da die mathematischen Grundlagen des maschinellen Lernens denen von 3D-Grafik oft ähneln, werden für Training und Betrieb von KI-Modellen oft Grafikkarten, so genannte GPUs eingesetzt. Diese benötigen durch die große Rechenkapazität sehr viel Energie. Aus dem Anschaffungspreis der GPUs, den Stromkosten und dem Co2-Fußabdurck, der bei der Stromproduktion entsteht, ergeben sich viele Debatten um die langrfistige Wirtschaftlichkeit und Klimaschutz von KI.
Der Transformer-Block
Der Kern der Verarbeitung des Transformers liegt im Transformer-Block, der aus Multi-Head-Selbst-Aufmerksamkeit und einer Multi-Layer-Perceptron-Schicht besteht. Die meisten GPT-Modelle bestehen aus mehreren solcher Blöcke, die sequentiell, also nacheinander ausgeführt werden. Bei GPT-2 kommen insgesamt 12 solcher Transformer-Blöche zum Einsatz. Die Token-Repräsentationen propagiert durch die Schichten, vom ersten Block bis zum zwölften, was dem Modell ermöglicht, ein komplexes Verständnis jedes Tokens aufzubauen. Dieser schichtweise Ansatz führt zu einem generalisierten Verständnis, oder mathematisch ausgedrückt, zu einem Verständnis höherer Ordnung.
Mehrköpfige Selbstaufmerksamkeit
Die bahnbrechende Innovation der Transformer-Architektur war die Einführung des Algorithmus der Simulation von menschlicher Aufmerksamkeit, die sich auf den Kontext der gesamten Verabreitung bezieht ("Selbstaufmerksamkeit" bzw. "Self-Attention").
Durch diesen Schritt in der Verarbeitung der Einbettungs-Vektoren beim Vorwärts-Durchlauf des künstlichen neuronalen Netzes wird die Wahrscheinlichkeit des jeweils nächsten Tokens durch ganze Token-Sequenzen, also Halbsätze, Sätze, Absätze usw. sowie deren geamte semantische Bedeutung beeinflusst. Erst durch diesen Algorithmus in Verbindung mit vielen, gut gewählten und für das Training aufbereiteten Textdaten ergibt sich eine deutlich bessere Qualität der generierten Texte im Vergleich zu vorherigen Versuchen, Text-generierende Sprachmodelle zu entwickeln.
Es ist außerdem wichtig zu verstehen, dass die Verarbeitung der Token-Sequenzen in den Transformer-Blöcken nicht linear erfolgt, sondern durch die Selbstaufmerksamkeit eine komplexe, nicht-lineare Verarbeitung der Token-Sequenzen stattfindet. Wäre die Verarbeitung linear, könnte das Modell keine komplexen Beziehungen und Abhängigkeiten innerhalb der Daten erfassen. Außerdem wäre es sinnlos, 12 Transformer-Blöcke hintereinander auszuführen, wenn sie jeweils die gleichen Ergebnisse liefern würden.
Des Weiteren ist es essenziell zu verstehen, dass der Transformer-Block sowohl beim Training (also während der Backpropagation) als auch bei der Inferenz (also der Text-Generierung) zum Einsatz kommt, jedoch auf unterschiedliche Weise. Während des Trainings wird die Selbstaufmerksamkeit dazu verwendet, um das Modell zu zwingen, sich beim Optimieren des Modells auf relevante Teile des Eingabetextes zu konzentrieren, während bei der Inferenz die Selbstaufmerksamkeit dazu dient, die generierten Token-Sequenzen zu überprüfen und gegebenenfalls anzupassen.
Um die Funktionsweise des Transformer-Blocks besser zu verstehen, schauen wir uns nun einmal an, wie die Selbstaufmerksamkeit Schritt für Schritt berechnet wird:
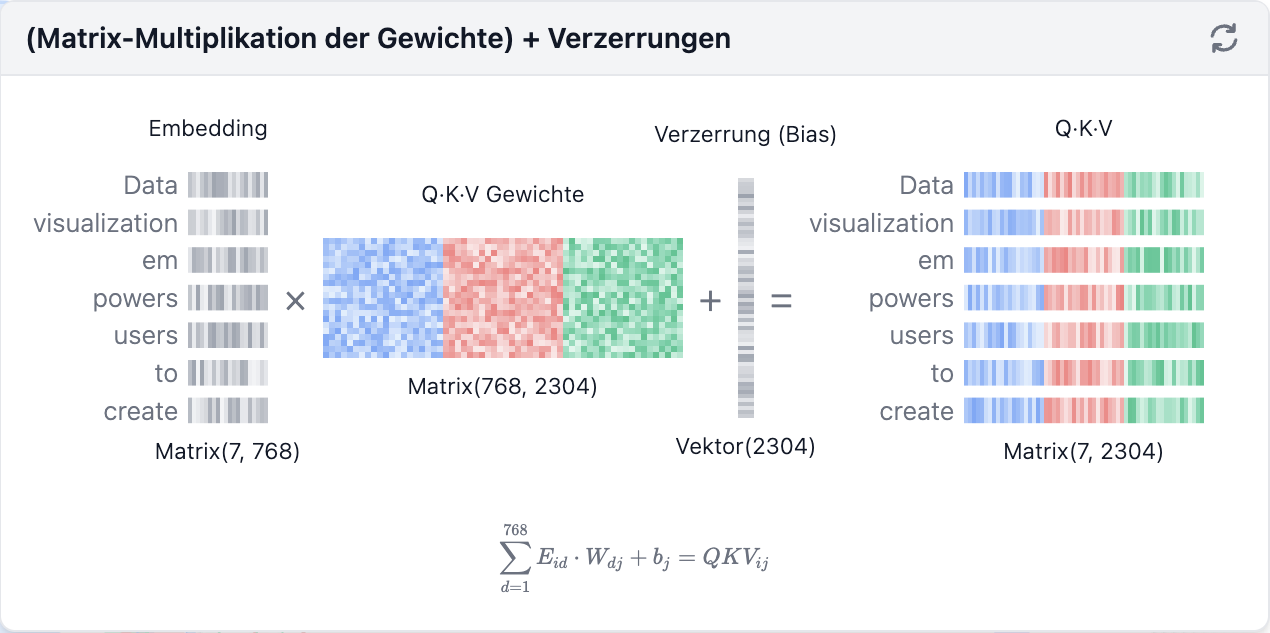
Schritt 1: Anfrage- (Q), Schlüssel- (K), und Wert- (V) Matritzen berechnen
Jede Vektor-Einbettung, die einem Eingabe-Token zugeordnet ist (siehe Abschnitt "Vektor-Einbettungen"), wird in drei verschiedene Vektoren umgewandelt: Anfrage (Q)-Vektor, Schlüssel (K)-Vektor und Wert (V)-Vektor. Diese Vektoren entstehen, indem der Einbettungs-Vektor mit den globalen, während des Trainings gelernten Gewichtsmatrizen für Q, K und V multipliziert wird. Um besser zu verstehen, wofür diese Vektoren stehen, hilft ein Vergleich mit einer Websuche:
- Anfrage (Q) wäre ein Suchbegriff, den Sie in die Suchmaschine eingeben. Er entspricht dem Token, über das Sie "mehr wissen möchten".
- Schlüssel (K) ist der Titel jeder Webseite in der Ergebnisliste. Er steht für die möglichen Tokens, auf die sich die Suchanfrage möglicherweise beziehen könnte.
- Wert (V) ist der eigentliche Inhalt der Webseiten. Nachdem der passende Suchbegriff (Anfrag) mit den relevanten Ergebnissen (Werten) verknüpft wurde, möchten wir den Inhalt (Wert) der relevantesten Seiten abrufen.
Durch die Verwendung dieser QKV-Werte kann das Modell Aufmerksamkeitswerte berechnen, die bestimmen, wie stark sich das Modell auf jedes Token konzentrieren soll.
Schlussendlich wird für jeden der Vektoren – Anfrage (Q), Schlüssel (K) und Wert (V) – eine Verzerrung hinzugefügt, indem der jeweilige Verzerrungsvektor, der während des Trainings gelernt wurde, auf die einzelnen Vektoren addiert wird. Diese Verzerrungsvektoren sind lernbare Parameter, die es dem Modell ermöglichen, nichtlineare Beziehungen zwischen den Tokens zu erfassen und zu generalisieren, wodurch das Modell flexibler auf unterschiedliche Eingaben reagieren kann.
Abschließend ergibt sich für jeden Token (genauer genommen, für jeden Einbettungs-Vektor jeden Tokens) ein Satz von drei Vektoren: ein gewichteter und verzerrter Anfrage-Vektor (Q), ein gewichteter und verzerrter Schlüssel-Vektor (K) sowie ein gewichteter und verzerrter Wert-Vektor (V).
Schritt 2: Maskierte Selbstaufmerksamkeit
Die maskierte Selbstaufmerksamkeit ermöglicht es dem Modell, Sequenzen zu generieren, indem es sich auf relevante Teile der Eingabe konzentriert, ohne auf zukünftige Tokens zuzugreifen.
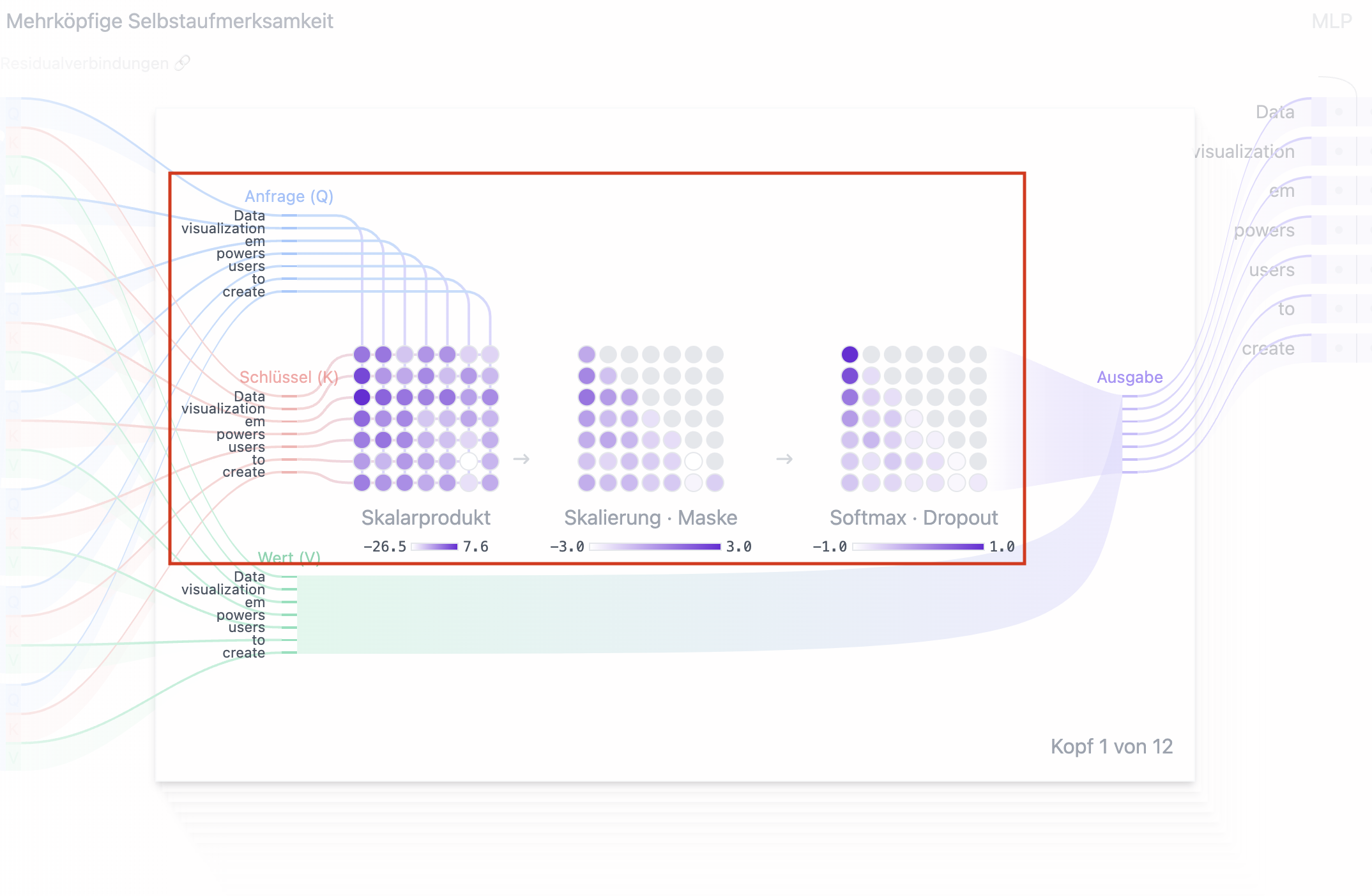
Skalarprodukt: Zunächst wird der gewichtete und verzerrte Anfrage-Vektor (Q) eines Tokens mit den gewichteten und verzerrten Schlüssel-Vektoren (K) aller Tokens in der Sequenz multipliziert. Diese Matrix-Multiplikation erzeugt eine Ergebnismatrix, bei der jede Zahl das Skalarprodukt bzw. Punktprodukt zwischen dem Q-Vektor und einem K-Vektor darstellt. Dieses Produkt misst die Ähnlichkeit zwischen der Anfrage und den Schlüsseln. Das Ergebnis für jedes Paar von Q und K in der Matrix gibt an, wie stark die Aufmerksamkeit des Modells auf das jeweilige Token gerichtet werden sollte.
Skalierung: Um sicherzustellen, dass die Werte in einem geeigneten Bereich liegen und die Berechnungen stabil bleiben, wird das Ergebnis durch die Quadratwurzel der Dimension der Vektoren skaliert. Diese Maßnahme sorgt dafür, dass die resultierenden Aufmerksamkeitswerte nicht zu groß werden.
Maskierung: Als nächstes wird eine Maske auf das obere Dreieck der Ergebnismatrix angewendet, um zu verhindern, dass das Modell auf zukünftige Tokens zugreift. Dabei werden alle Werte, die zukünftige Tokens repräsentieren, auf negative Unendlichkeit gesetzt. Dieser Schritt ist notwendig, um sicherzustellen, dass das Modell sowohl beim Training als auch bei der Inferenz das nächste Token nur basierend auf den bereits bekannten (d.h. vorherigen) Tokens vorhersagt, ohne auf Informationen zuzugreifen, die in der Zukunft liegen.
Softmax-Funktion: Anschließend werden die skalierten Werte durch eine Softmax-Funktion verarbeitet. Die Softmax-Funktion sorgt dafür, dass alle Aufmerksamkeitswerte für jede Zeile der Ergebnismatrix (also jeden Token) in Wahrscheinlichkeiten umgewandelt werden, die zusammen 1 ergeben (also insgesamt 100% entsprechen). So wird sichergestellt, dass das Modell seine Aufmerksamkeit proportional auf die relevanten Einabe-Tokens verteilt.
Dropout: Das Dropout-Verfahren deaktiviert zufällig ausgewählte Neuronen in den versteckten Schichten des neuronalen Netzes, um Überanpassung zu vermeiden. (siehe Abschnitt: "Typische Probleme beim Lernprozess: Über- und Unteranpassung"). Beim Training wird Dropout angewendet, um das Modell zu zwingen, nicht zu stark von einzelnen Neuronen abhängig zu sein und stattdessen robustere, generalisierte Merkmale zu lernen. Bei der Inferenz kommt Dropout jedoch nicht zum Einsatz, da es hier keinen Sinn ergibt, zufällige Neuronen zu deaktivieren. Das Modell kann ja bereits generalisieren und würde man bei der Inferenz Dropout aktivieren, käme es zu einer zufälligen Verfälschung der generierten Text-Sequenzen.
Schritt 3: Berechnung der Ausgabe
Die Aufmerksamkeitswahrscheinlichkeiten, die für jedes Token in der Eingabesequenz mittels der Softmax-Funktion erzeugt wurden, werden verwendet, um die (bereits im vorherigen Schritt global gewichteten und verzerrten) Wert-Vektoren (V) zusätzlich noch Aufmerksamkeits-bezogen zu gewichten. Für jedes Token in der Sequenz wird der Wert-Vektor jedes anderen Tokens mit dem entsprechenden Aufmerksamkeitswert multipliziert. Diese Aufmerksamkeits-gewichteten Wert-Vektoren werden dann für jedes Token summiert, um einen neuen Vektor für dieses Token zu erzeugen. Dieser neue Vektor repräsentiert das finale Ergebnis für das jeweilige Token, basierend auf der gewichteten Summe der Informationen von allen anderen Tokens in der Sequenz.
Das Ergebnis dieser Berechnung ist eine Liste von Vektoren, wobei jeder Vektor die finale Repräsentation eines Tokens aus der Eingabesequenz darstellt:
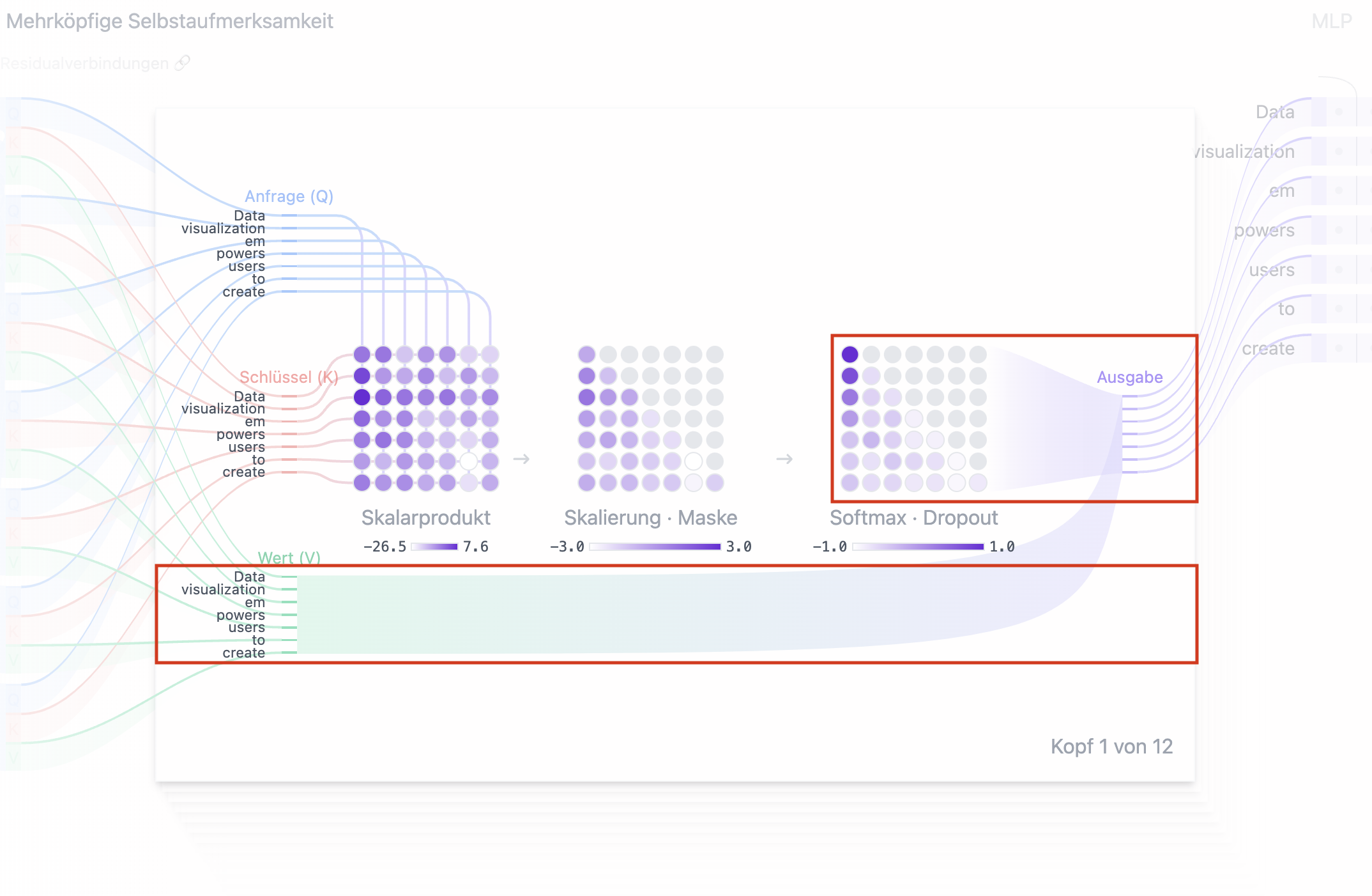
Bei Modellen, die wie GPT-2, über 12 Köpfe für die Selbstaufmerksamkeit verfügen, wird dieser Prozess parallel für jeden Kopf durchgeführt (vgl. "Kopf 1 von 12").
Jeder Kopf erfasst dabei unterschiedliche Beziehungen zwischen den Tokens der Eingabe. Die Ausgabe dieser Köpfen, also die Listen der aufmerksamkeitsgewichteten Vektoren,
wird anschließend zusammengeführt (konkateniert) und durch eine lineare Projektion weiterverarbeitet, um das finale Gesamtergebnis
des Selbstaufmerksamkeits-Mechanismus über alle Köpfe hinweg zu erhalten.
Das finale Gesamtergebnis ist eine Liste von gewichteten Vektoren, die die kombinierten Informationen aus allen Selbstaufmerksamkeits-Köpfen enthalten. Jeder Vektor in der Liste bezieht sich dabei weiterhin auf einen Token in der Eingabesequenz. Diese Liste von gewichteten Vektoren bildet die Grundlage für die weitere Verarbeitung im Multi-Layer Perceptron (MLP) des Transformer-Blocks.
Mehrlagiges Perzeptron (MLP)
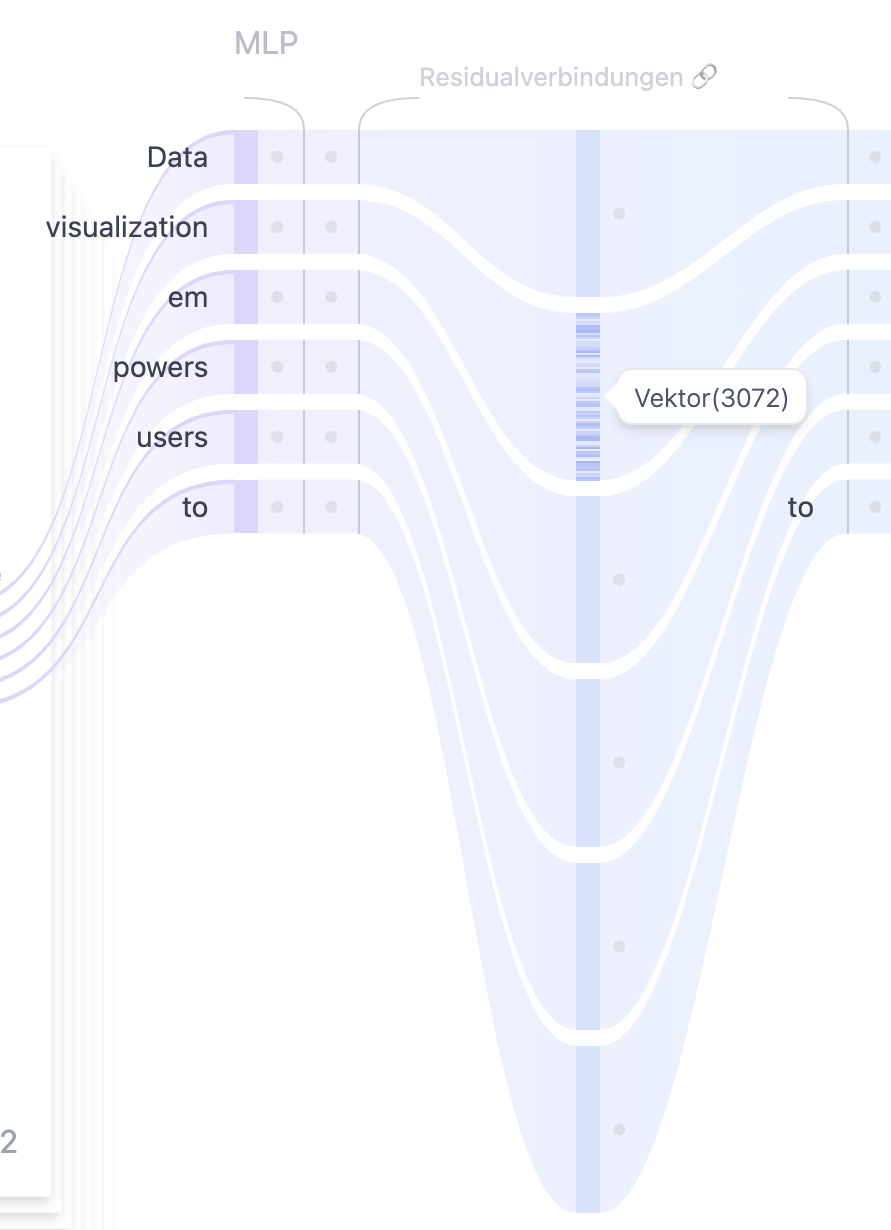
Nachdem die verschiedenen Köpfe des Selbstaufmerksamkeits-Mechanismus die unterschiedlichen Beziehungen zwischen den Eingabe-Tokens erfasst haben, werden die zusammengefügten Ergebnisse durch eine Schicht namens Multilayer Perceptron (MLP) geleitet, um die Fähigkeit des Modells, komplexe Zusammenhänge zu verstehen, weiter zu verbessern. Der MLP-Block besteht aus zwei aufeinanderfolgenden linearen Transformationen, zwischen denen eine Aktivierungsfunktion namens GELU liegt.
Bei der ersten Transformation wird die Dimensionalität der Eingabedaten vervierfacht, also von 768 auf 3072 erhöht.
Anschließend reduziert die zweite Transformation die Dimensionalität wieder auf die ursprüngliche Größe von 768, damit die nächsten Schichten im Modell weiterhin mit Daten in der selben Dimensionalität arbeiten können.
Die GELU-Aktivierungsfunktion, die zwischen diesen beiden Transformationen liegt, fügt eine wichtige Nichtlinearität hinzu. Das MLP, wie auch die anderen Teile des Modells, wird während des Trainingsprozesses durch Gradient Descent optimiert. Bei der Inferenz wird das MLP lediglich durchlaufen, um die bereits gelernten Transformationen auf die Eingabedaten anzuwenden.
Im Gegensatz zum Selbstaufmerksamkeits-Mechanismus, der die Beziehungen zwischen den Tokens berücksichtigt, verarbeitet das MLP jedes Token unabhängig voneinander und wandelt es einfach von einer Darstellung in eine andere um. Durch die Kombination der Nichtlinearität und der Dimensionserweiterung kann das MLP komplexere Merkmale und Zusammenhänge erfassen.
Vorhersage des besten, nächsten Token
Nachdem die Eingabedaten alle Transformer-Blöcke durchlaufen haben, erhält jedes Token in der Sequenz einen finalen Vektor, der als "finale Repräsentation" bezeichnet wird. Diese Repräsentationen fassen die Bedeutung und den Kontext jedes Tokens zusammen, basierend auf den Beziehungen zu den anderen Tokens und den Merkmalen, die das Modell durch die Verarbeitung gelernt hat. Die finalen Repräsentationen sind das Ergebnis der Anwendung von Selbstaufmerksamkeits-Mechanismen und allen weiteren Transformationen in den Transformer-Blöcken.
Diese finalen Repräsentationen werden anschließend durch eine letzte lineare Schicht geleitet, um sie für die Token-Vorhersage
vorzubereiten. Die letzte Schicht projiziert die Repräsentationen in einen 50.257-dimensionalen Raum,
also einen Raum, der so groß ist, wie das Vokabular des Tokenizers.
Dabei erhält jedes Token im Vokabular einen entsprechenden Scoring-Wert, der als Logit bezeichnet wird.
Da jedes Token das nächste Wort in der Sequenz sein könnte, ermöglicht uns dieser Prozess, die Tokens nach ihrer Wahrscheinlichkeit,
das gesuchte nächste Wort zu sein, zu sortieren.
Hierfür wird wieder die Softmax-Funktion angewendet, um die Logits in eine Wahrscheinlichkeitsverteilung umzuwandeln,
die sich auf eins (also ingesamt 100%) aufsummiert.
Mittels dieser Wahrscheinlichkeitsverteilung kann nun das gesuchte nächste Token auszuwählt werden.
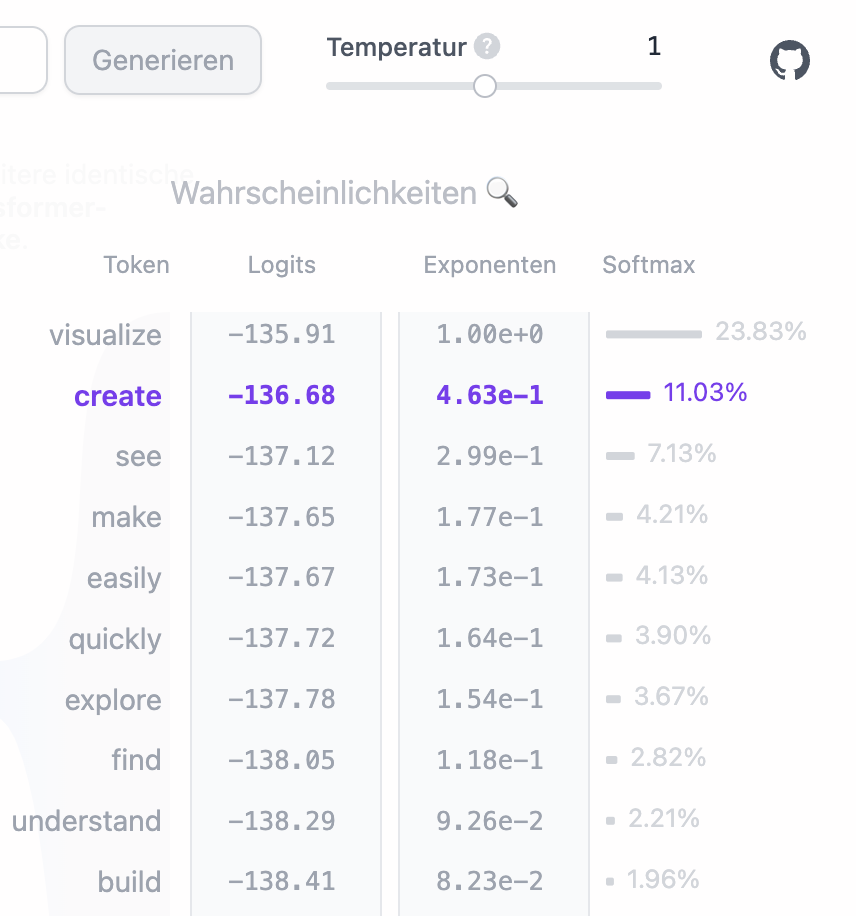
Der letzte Schritt besteht darin, das nächste Token durch Sampling aus dieser Verteilung zu erzeugen.
Der Inferenz-Hyperparameter temperature (Temperatur) spielt dabei eine entscheidende Rolle.
Mathematisch gesehen ist das eine sehr einfache Operation: Die Ausgabe-Logits des Modells werden einfach durch den
temperature-Wert dividiert:
temperature = 1: Die Division der Logits durch eins hat keinen Effekt auf die Softmax-Ausgaben.temperature < 1: Eine niedrigere Temperatur macht das Modell selbstsicherer und deterministischer, indem die Wahrscheinlichkeitsverteilung geschärft wird, was zu vorhersehbareren Ausgaben führt.temperature > 1: Eine höhere Temperatur erzeugt eine weichere Wahrscheinlichkeitsverteilung, was mehr Zufälligkeit im erzeugten Text ermöglicht. Manche würden das als "kreativer" empfinden.
Stellen Sie doch mal den Temperatur-Hyperparameter anders ein. So können Sie interaktiv herausfinden, wie sich das Gleichgewicht zwischen deterministischen und vielfältigen Ausgaben verhält.
Textausgabe: Vielleicht ist Ihnen bereits aufgefallen, dass nun auch die jeweilige Token-ID wieder bekannt ist. Wir können also einfach im Vokabular des Tokenizers nachsehen, welches Wort, Teilwort oder Zeichen der letztlich gewählten Token-ID entspricht. So wird die Token-ID in eine sinnvolle Textausgabe zurückverwandelt.
Wie funktioniert diese Website?
Das GPT-2-Modell (kleine Variante, 4 Bit-quantisiert) wird gerade lokal auf Ihrem Gerät und direkt hier im im Webbrowser ausgeführt. Dieses Modell wurde vom der PyTorch-Implementierung des selben GPT-Modells abgeleitet, das Andrej Karpathy mit seinem nanoGPT-Projekt entwickelt hat und das GPT-2 nachempfunden ist. Das Modell wurde so konvertiert, dass es mit der KI-Modell-Laufzeitumgebung ONNX funktioniert, die eine nahtlose Ausführung mittels WebAssembly und WebGPU im Browser ermöglicht. Die Benutzeroberfläche ist mit JavaScript, und dem Svelte Weboberflächen-Framework erstellt worden. Die Visualisierungen basieren auf D3.js, einem Framework für interaktive und dynamische Datenvisualisierungen. Die numerischen Werte werden live aktualisiert, sobald sich die Eingabe ändert. Die Textgenerierung erfolgt dabei in Echtzeit.